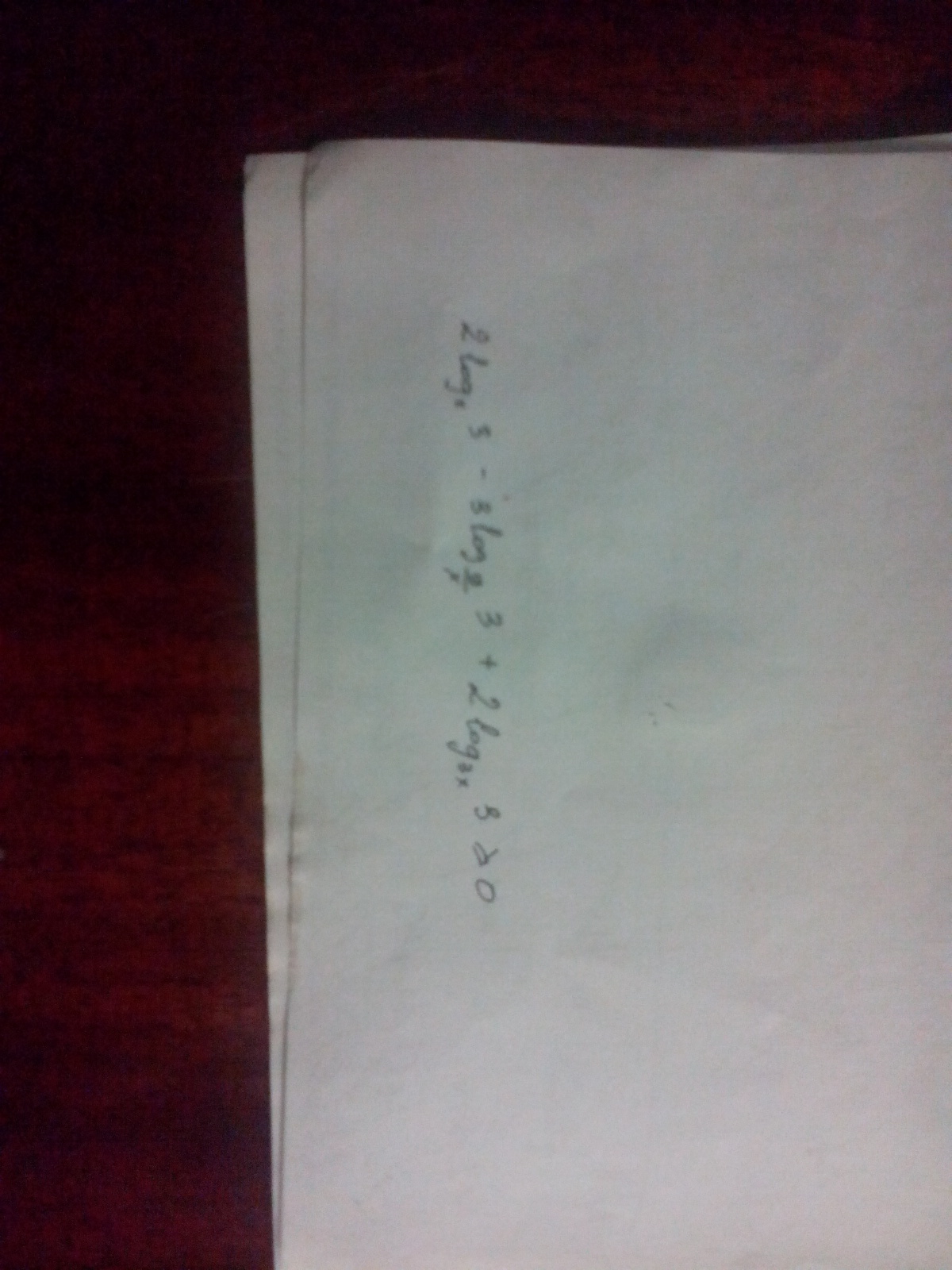Ответы
Ответ дал:
0
ОДЗ:
x > 0; x≠1
9/x >0; 9/x≠1
3x >0; 3x≠1
(0;1/3)U(1/3;1)U(1;9)U(9;+∞)
Переходим к основанию 3:

Применяем
1) log₃3=1
2) логарифм частного равен разности логарифмов
3) логарифм произведения равен сумме логарифмов

Замена переменной
log₃x=t

Метод интервалов:
___-___(-1)_+__[-4/7]__-__(0)__+__[1]__-__(2)__+__
-1 < t≤-4/7
0 < t≤1
t≥2
-1 < log₃x ≤ - 4/7
0 < log₃x ≤1
log₃x ≥ 2
-1·log₃3 < log₃x ≤ - 4/7·log₃3
log₃1 < log₃x ≤log₃3
log₃x ≥ 2·log₃3
log₃3⁻¹ < log₃x ≤ log₃3⁻⁴/⁷
log₃1 < log₃x ≤log₃3
log₃x ≥ log₃3²
3⁻¹ < x ≤ 3⁻⁴/⁷
1 < x ≤3
x ≥ 9
C учетом ОДЗ получаем ответ:
\\ \\\\\\\\\\\\ \\\\\\\\\
(0)_(1/3)__[1/⁷√3⁴]____(1)____________[3]______________(9)_____
(1/3; 1/ (⁷√3⁴)]U(1;3]U(9;+∞)
x > 0; x≠1
9/x >0; 9/x≠1
3x >0; 3x≠1
(0;1/3)U(1/3;1)U(1;9)U(9;+∞)
Переходим к основанию 3:
Применяем
1) log₃3=1
2) логарифм частного равен разности логарифмов
3) логарифм произведения равен сумме логарифмов
Замена переменной
log₃x=t
Метод интервалов:
___-___(-1)_+__[-4/7]__-__(0)__+__[1]__-__(2)__+__
-1 < t≤-4/7
0 < t≤1
t≥2
-1 < log₃x ≤ - 4/7
0 < log₃x ≤1
log₃x ≥ 2
-1·log₃3 < log₃x ≤ - 4/7·log₃3
log₃1 < log₃x ≤log₃3
log₃x ≥ 2·log₃3
log₃3⁻¹ < log₃x ≤ log₃3⁻⁴/⁷
log₃1 < log₃x ≤log₃3
log₃x ≥ log₃3²
3⁻¹ < x ≤ 3⁻⁴/⁷
1 < x ≤3
x ≥ 9
C учетом ОДЗ получаем ответ:
\\ \\\\\\\\\\\\ \\\\\\\\\
(0)_(1/3)__[1/⁷√3⁴]____(1)____________[3]______________(9)_____
(1/3; 1/ (⁷√3⁴)]U(1;3]U(9;+∞)
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад