Найти мах целое значение параметра а при котором уравнение имеет 2 корня
[x+3](x-3) разделить на а-3 =1
х+3 под знаком модуль
Ответы
Ответ дал:
0
Запишем уравнение в виде
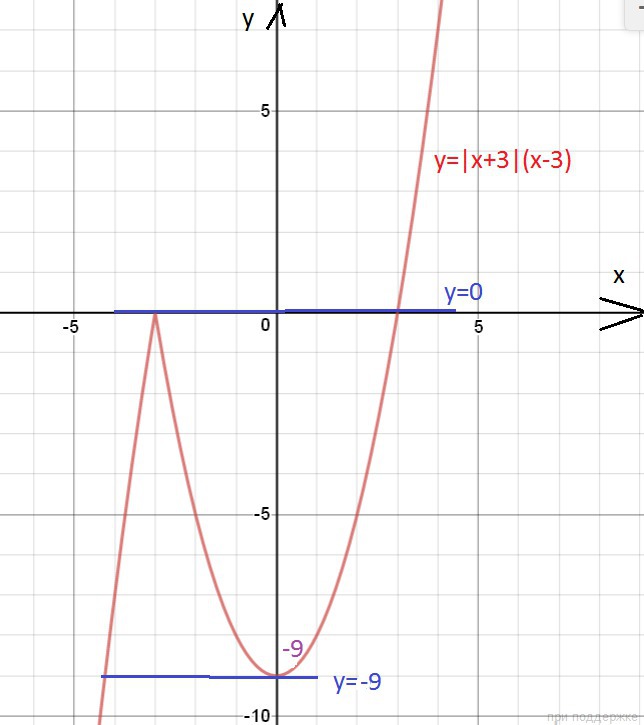
|x+3|(x-3)=a-3
а≠3
Строим график функции
у=|x+3|(x-3)
На (-∞;-3)
|x+3|=-x-3
cтроим график у=-х²+9
на [-3;+∞)
|x+3|=x+3
строим график у=х²-9
График функции у=a-3 при разных значения а - прямые, параллельные оси ох.
Графики такого вида пересекаются с графиком у=|x+3|(x-3) в двух точка только в двух случаях
a-3=0, но по условию а≠3
или
a-3=-9 ⇒ а=-6
О т в е т. при а = - 6
|x+3|(x-3)=a-3
а≠3
Строим график функции
у=|x+3|(x-3)
На (-∞;-3)
|x+3|=-x-3
cтроим график у=-х²+9
на [-3;+∞)
|x+3|=x+3
строим график у=х²-9
График функции у=a-3 при разных значения а - прямые, параллельные оси ох.
Графики такого вида пересекаются с графиком у=|x+3|(x-3) в двух точка только в двух случаях
a-3=0, но по условию а≠3
или
a-3=-9 ⇒ а=-6
О т в е т. при а = - 6
Приложения:
Ответ дал:
0
Почему на графике при х=-3 линия графика идет вниз
Ответ дал:
0
Потому что это левая ветвь параболы у=-х²+9 и то не вся, а только ее часть.
Ответ дал:
0
На (-∞;-3)
|x+3|=-x-3
cтроим график у=-х²+9
|x+3|=-x-3
cтроим график у=-х²+9
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад