Две стороны треугольника равны 7√3 и 12 , а биссектрисы при третьей стороне пересекаются под углом 30 градусов. Найдите площадь треугольника.

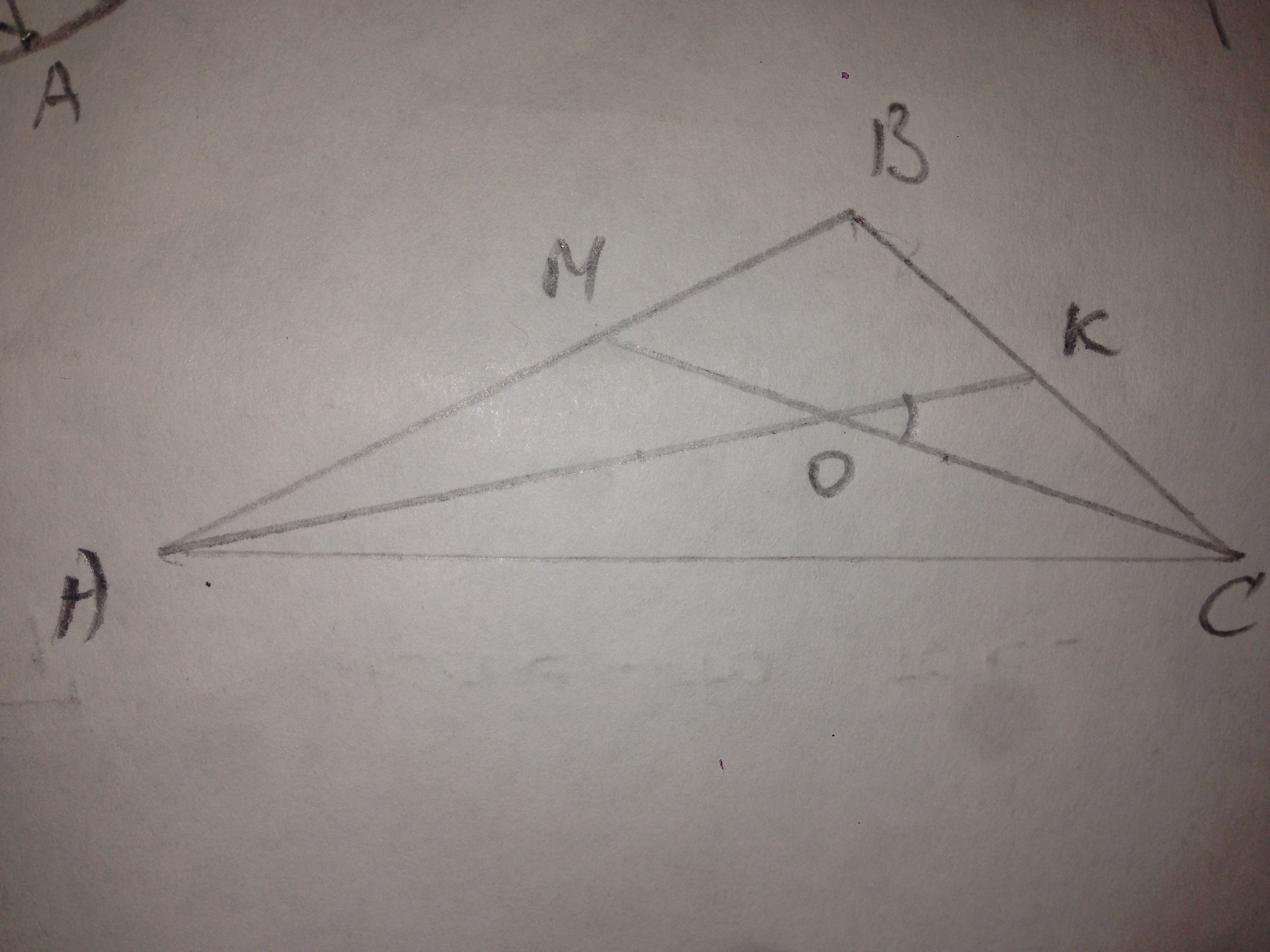
В тр-ке АВС АК и ВМ - биссектрисы. АВ=7√3, ВС=12, ∠КОС=30°.
В тр-ке АОС ∠САО+∠АСО=∠КОС=30°.
В тр-ке АВС ∠А+∠С=2(∠САО+∠АСО)=60° ⇒ ∠В=180-60=120°.
Площадь: S=0.5·AB·BC·sin120=0.5·7√3·12·√3/2=63 (ед²) - это ответ.