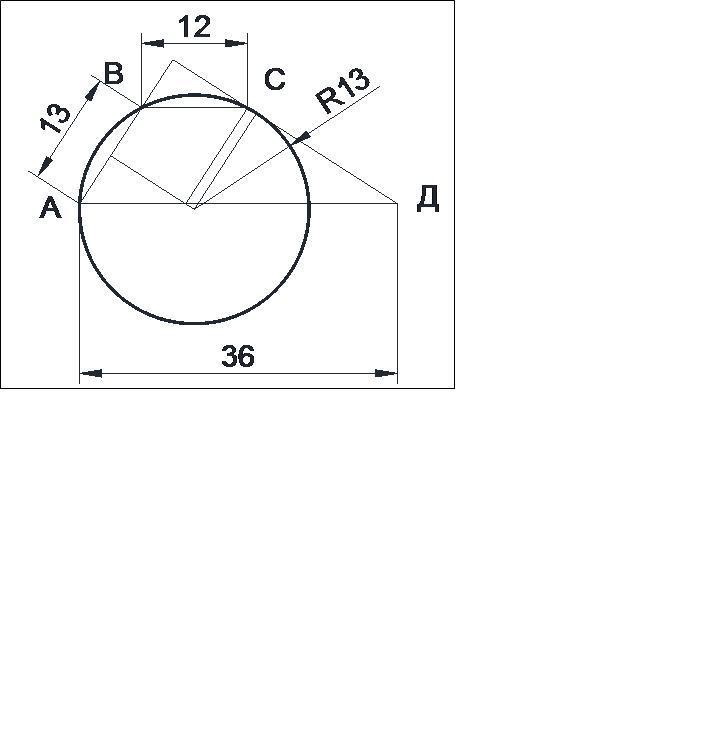
В трапеции ABCD основания AD и BC равны соответственно 36 и 12, а сумма углов при основании AD равна 90∘. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=13.
Ответы
Ответ дал:
0
Центр окружности, проходящей через точки A и B, лежит на срединном перпендикуляре стороны АВ.
Из точки С проведём отрезок СЕ параллельно АВ и равный, как и АВ, 13.
Поэтому срединный перпендикуляр стороны АВ параллелен СД.
Тогда радиус окружности, проходящей через точки A и B и касающейся прямой CD тоже равен 13.
Из точки С проведём отрезок СЕ параллельно АВ и равный, как и АВ, 13.
Поэтому срединный перпендикуляр стороны АВ параллелен СД.
Тогда радиус окружности, проходящей через точки A и B и касающейся прямой CD тоже равен 13.
Приложения:
Похожие вопросы
2 года назад
7 лет назад
9 лет назад
10 лет назад