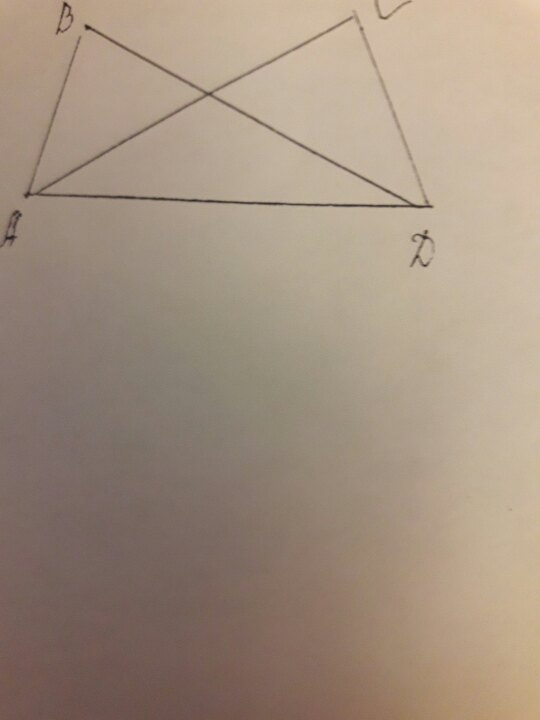
угол В= углу С= 90°, угол ADC=50°, угол ADB=40°. Докажите, что треугольник ABD= треугольнику DCA. (чертёж на фотографии)
ПОМОГИТЕ ПОЖАЛУЙСТА!!!
Приложения:
Ответы
Ответ дал:
0
1) ΔABD и ΔСDA - прямоугольные, так как ∠B = ∠C = 90°
2) в прямоугольном треугольнике сумма острых углов равна 90°
∠CAD + ∠ADC = 90°
∠CAD = 90° - ∠ADC = 90° - 50° = 40°
значит ∠CAD = ∠ADB = 40°
3) Рассмотрим прямоугольные ΔABD и ΔСDA:
AD - общая гипотенуза
∠CAD = ∠ADB (по доказательству)
значит ΔABD = ΔСDA по гипотенузе и острому углу
2) в прямоугольном треугольнике сумма острых углов равна 90°
∠CAD + ∠ADC = 90°
∠CAD = 90° - ∠ADC = 90° - 50° = 40°
значит ∠CAD = ∠ADB = 40°
3) Рассмотрим прямоугольные ΔABD и ΔСDA:
AD - общая гипотенуза
∠CAD = ∠ADB (по доказательству)
значит ΔABD = ΔСDA по гипотенузе и острому углу
Ответ дал:
0
∠САD=90°-50°=40°, ∠BAD=90°-40°=50° т е ΔABD=ΔACD по общей стороне и прилегающим углам
Похожие вопросы
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад