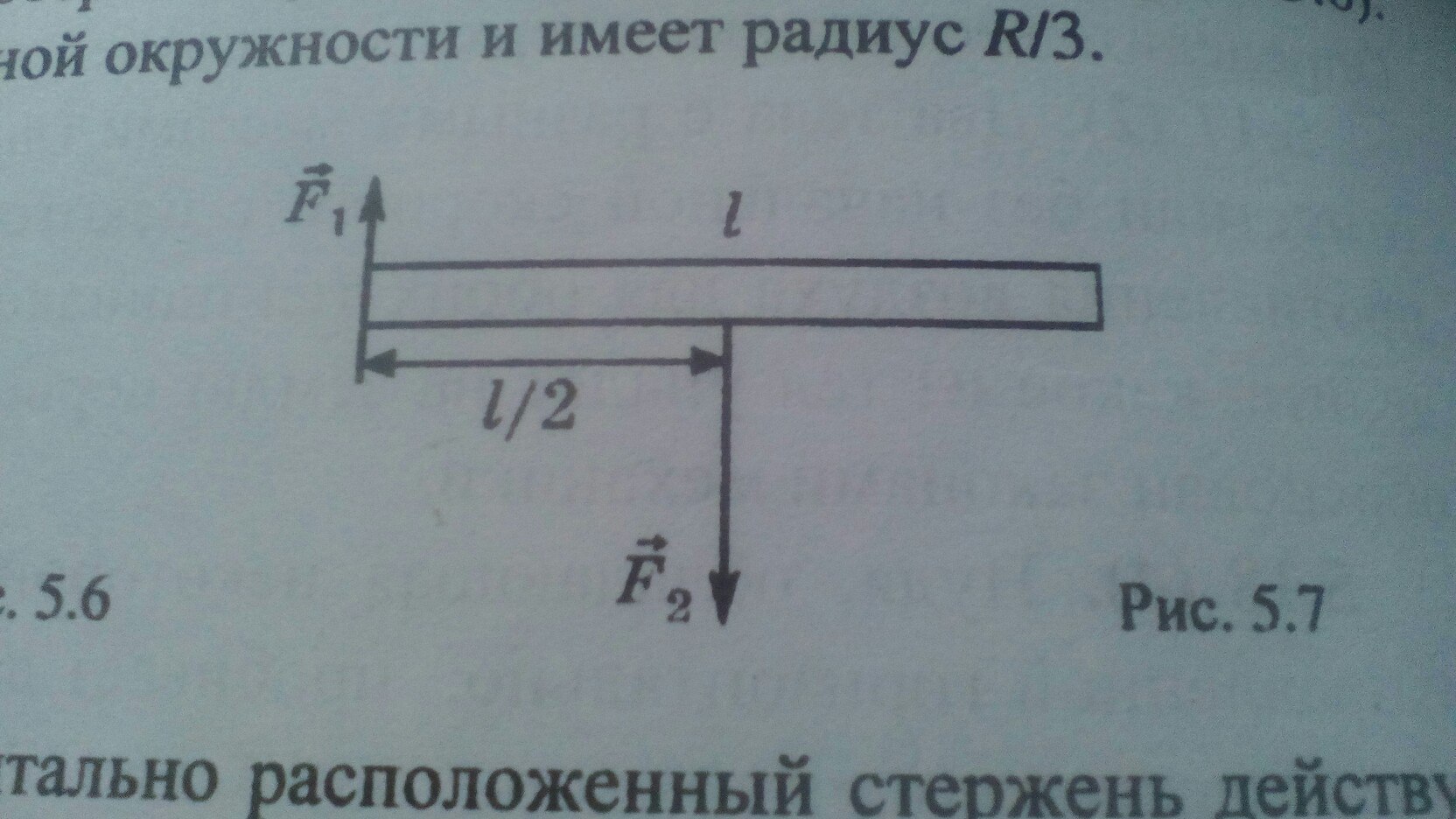
На горизонтально расположенный стержень действуют две параллельные силы, равные по величине F1 = 2 Н и F2 = 6 Н (рис. 5.7). Первая сила приложена к левому концу стержня и направлена вертикально вверх, вторая — к середине и направлена вертикально вниз. Определите величину и направление силы, уравновешивающей силы F1 и F2 , а также точку приложения этой силы.

1) Определим величину и направление силы.
Потребуем, что бы не перемещался центр масс системы.
Для этого в II законе ньютона добавим силу F
0 = F1 - F2 + F
F = 6 - 2 = 4 (Н)  и направлена вверх (я взял направление вверх за положительное направление оси z при проектировании).

2) Определим точку приложения силы.
Потребуем, что бы система не вращалась. Для этого суммарный момент системы должен быть равен нулю.

Отступление: Момент силы, это векторное произведение радиус вектора к точке, к которой приложена сила, и самой силы. М = [r×F]
Момент это вектор, амплитуда которого равна М = rFsinα. Здесь α - угол между векторами r и F. Вектор М ⊥ r и М ⊥ F. rsinα - плечо силы.
Если выполнено условие, что сумма всех сил в системе равна нулю, то не важно относительно какой точки отсчитывать момент.
т.е. плечо силы можно считать от любой точки.
Докажем это:
Пусть есть точка A и точка B.
Момент относительно точки A: 
Пусть 
Момент относительно точки B: 



Теперь, когда мы понимаем, что нам всё равно относительно какой точки считать момент, будем считать его от левого начала стержня.


Условие неподвижности стержня M = M₂. Отсюда следует:


Ответ: Сила величиной 4 Н, направлена вверх. Приложена к точке, отстоящей от левого края на (3/4)l