Задача: В четырёхугольник авсд вписана окружность с центром в точке о Найти величину угла aob если величина угла cod равна 94

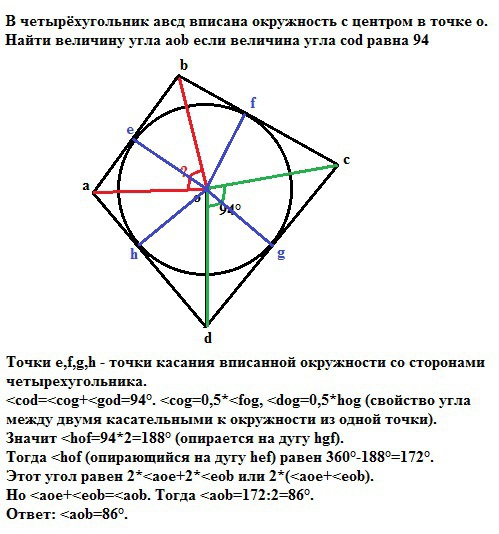
Точки e,f,g,h - точки касания вписанной окружности со сторонами четырехугольника.
<cod=<cog+<god=94° (дано). <cog=0,5*<fog, <dog=0,5*hog (свойство угла между двумя касательными к окружности из одной точки - co и do являются биссектрисами углов <fog и <goh).
Значит <hof=94*2=188° (опирается на дугу hgf).
Тогда <hof (опирающийся на дугу hef) равен 360°-188°=172°.
Этот угол равен 2*<aoe+2*<eob или 2*(<aoe+<eob) по указанному выше свойству.
Но <aoe+<eob=<aob. Тогда <aob=172:2=86°.
Ответ: <aob=86°.