16
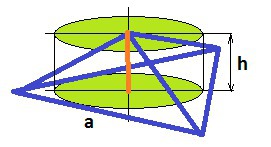
В основании пирамиды лежит правильный треугольник. В него вписана окружность, являющаяся основанием цилиндра той же высоты, что и пирамида. Найдите объём пирамиды, если объём цилиндра равен Вариант 1

Радиус вписанной окружности в равнобедренный треугольник по формуле:
r² = (p-a)³/p, где: р = 3/2*а - полупериметр, а - сторона основания.
Преобразуем
r² = 1/8*а³ : 3/2*а = а²/12 - оставим в таком виде
Объем пирамиды по формуле:
Vпир = 1/3 * S*h - 
Объем цилиндра по формуле
Vцил = π*r² *h 
Отсюда
h = V : (πr²) = V: (π*a²/12) = (12*V)/(πa²) - высота пирамиды
Остается вычислить Sосн равностороннего треугольника по формуле 
Sосн = √3/4*а²
Подставим в формулу объема пирамиды и получим (?)
Vпир = (1/3)*(√3/4*а²)*(12V/(πа²))=   √3*V= √3 ~ 1.73 - ОТВЕТ