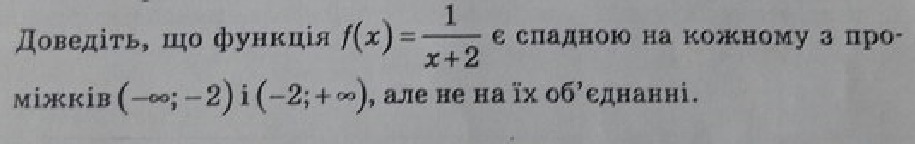Ответы
Ответ дал:
0
Дана функция 
Доказать что функция убывает на промежутке (-∞:-2)(-2:+∞)
Заметим сразу что ОДЗ (-∞:-2)(-2;+∞), так как в точке х=-2 функция не определена.
Для того чтобы найти промежутки убывания или возрастания функции необходимо найти ее производную и определить знаки производной.

Мы видим что в точке х=-2 производная не существует.
Рассмотрим значение производной на области допустимых значений.
Легко видеть, что знаменатель при любых х будет всегда положительным числом, а числитель равен -1. Значит значение производной на всей обрасти допустимых значений отрицательное число.
А значит функция Убывающая на всей области допустимых значений.
Доказать что функция убывает на промежутке (-∞:-2)(-2:+∞)
Заметим сразу что ОДЗ (-∞:-2)(-2;+∞), так как в точке х=-2 функция не определена.
Для того чтобы найти промежутки убывания или возрастания функции необходимо найти ее производную и определить знаки производной.
Мы видим что в точке х=-2 производная не существует.
Рассмотрим значение производной на области допустимых значений.
Легко видеть, что знаменатель при любых х будет всегда положительным числом, а числитель равен -1. Значит значение производной на всей обрасти допустимых значений отрицательное число.
А значит функция Убывающая на всей области допустимых значений.
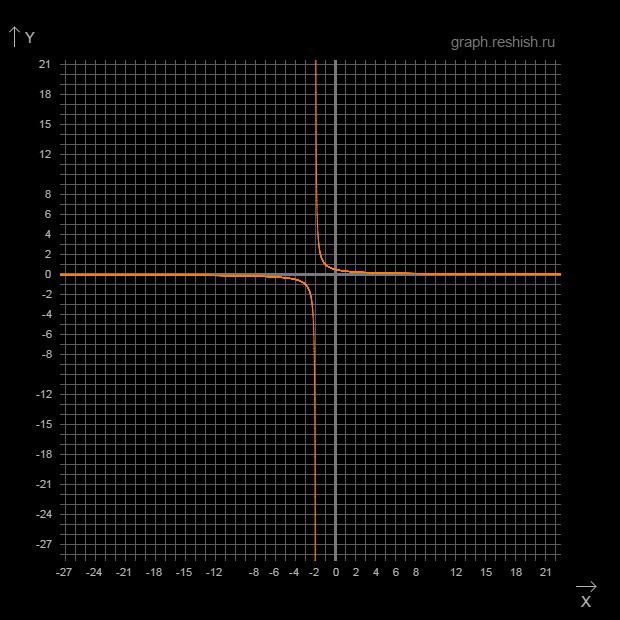
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад