Очень прошу решить этот пример: тема лимиты, решала разными способами, но ответы получаются разные. Проверила на wolframalpha, ответ -1, а как решить не знаю. Помогите пожалуйста!
Если что - это задачник Бермана "Сборник задач по курсу мат. анализа", номер 289)
Приложения:
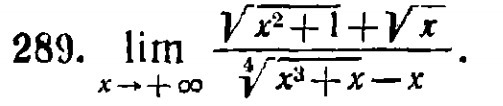
Ответы
Ответ дал:
0
Подставляем х в функцию и получаем неопределённость вида 
Определяем "икс" в старшей степени и затем делим числитель и знаменатель на него.
![lim_{xto infty} frac{ sqrt{x^2+1}+ sqrt{x} }{ sqrt[4]{x^3+x}-x}= frac{ {infty} }{{infty}}=](https://tex.z-dn.net/?f=+lim_%7Bxto+infty%7D++frac%7B+sqrt%7Bx%5E2%2B1%7D%2B+sqrt%7Bx%7D++%7D%7B+sqrt%5B4%5D%7Bx%5E3%2Bx%7D-x%7D%3D+frac%7B+%7Binfty%7D+%7D%7B%7Binfty%7D%7D%3D "lim_{xto infty} frac{ sqrt{x^2+1}+ sqrt{x} }{ sqrt[4]{x^3+x}-x}= frac{ {infty} }{{infty}}=")
(*)
(*)
![= lim_{x to infty} frac{frac{ sqrt{x^2+1}+ sqrt{x}}{x} }{frac{ sqrt[4]{x^3+x}-x}{x}}= lim_{x to infty} frac{ frac{ sqrt{x^2+1} }{x}+ frac{ sqrt{x} }{x} }{ frac{ sqrt[4]{x^3+x}}{x} - frac{x}{x} } = lim_{x to infty} frac{ frac{ sqrt{x^2+1} }{ sqrt{x^2} }+ frac{ sqrt{x} }{ sqrt{x^2} } }{ frac{ sqrt[4]{x^3+x}}{ sqrt[4]{x^4} } -1} =](https://tex.z-dn.net/?f=%3D+lim_%7Bx+to+infty%7D+++frac%7Bfrac%7B+sqrt%7Bx%5E2%2B1%7D%2B+sqrt%7Bx%7D%7D%7Bx%7D+%7D%7Bfrac%7B+sqrt%5B4%5D%7Bx%5E3%2Bx%7D-x%7D%7Bx%7D%7D%3D+lim_%7Bx+to+infty%7D++frac%7B+frac%7B+sqrt%7Bx%5E2%2B1%7D+%7D%7Bx%7D%2B+frac%7B+sqrt%7Bx%7D+%7D%7Bx%7D++%7D%7B+frac%7B+sqrt%5B4%5D%7Bx%5E3%2Bx%7D%7D%7Bx%7D+-+frac%7Bx%7D%7Bx%7D+%7D+%3D+lim_%7Bx+to+infty%7D++frac%7B+frac%7B+sqrt%7Bx%5E2%2B1%7D+%7D%7B+sqrt%7Bx%5E2%7D+%7D%2B+frac%7B+sqrt%7Bx%7D+%7D%7B+sqrt%7Bx%5E2%7D+%7D++%7D%7B+frac%7B+sqrt%5B4%5D%7Bx%5E3%2Bx%7D%7D%7B+sqrt%5B4%5D%7Bx%5E4%7D+%7D+-1%7D+%3D "= lim_{x to infty} frac{frac{ sqrt{x^2+1}+ sqrt{x}}{x} }{frac{ sqrt[4]{x^3+x}-x}{x}}= lim_{x to infty} frac{ frac{ sqrt{x^2+1} }{x}+ frac{ sqrt{x} }{x} }{ frac{ sqrt[4]{x^3+x}}{x} - frac{x}{x} } = lim_{x to infty} frac{ frac{ sqrt{x^2+1} }{ sqrt{x^2} }+ frac{ sqrt{x} }{ sqrt{x^2} } }{ frac{ sqrt[4]{x^3+x}}{ sqrt[4]{x^4} } -1} =")
![=lim_{x to infty} frac{ sqrt frac {{x^2+1} }{{x^2} }+{ sqrtfrac{{x} }{{x^2}} } }{ sqrt[4]{ frac{x^3+x}{x} } -1}= lim_{x to infty} frac{ sqrt{1+ frac{1}{x^2} }+ sqrt{ frac{1}{x} } }{ sqrt[4]{ frac{1}{x}+ frac{1}{x^3} }-1 } = frac{1}{-1}=-1](https://tex.z-dn.net/?f=%3Dlim_%7Bx+to+infty%7D++frac%7B++sqrt+frac+%7B%7Bx%5E2%2B1%7D+%7D%7B%7Bx%5E2%7D+%7D%2B%7B+sqrtfrac%7B%7Bx%7D+%7D%7B%7Bx%5E2%7D%7D+%7D++%7D%7B+sqrt%5B4%5D%7B+frac%7Bx%5E3%2Bx%7D%7Bx%7D+%7D+-1%7D%3D+lim_%7Bx+to+infty%7D++frac%7B+sqrt%7B1%2B+frac%7B1%7D%7Bx%5E2%7D+%7D%2B+sqrt%7B+frac%7B1%7D%7Bx%7D+%7D++%7D%7B+sqrt%5B4%5D%7B+frac%7B1%7D%7Bx%7D%2B+frac%7B1%7D%7Bx%5E3%7D++%7D-1+%7D+%3D+frac%7B1%7D%7B-1%7D%3D-1+ "=lim_{x to infty} frac{ sqrt frac {{x^2+1} }{{x^2} }+{ sqrtfrac{{x} }{{x^2}} } }{ sqrt[4]{ frac{x^3+x}{x} } -1}= lim_{x to infty} frac{ sqrt{1+ frac{1}{x^2} }+ sqrt{ frac{1}{x} } }{ sqrt[4]{ frac{1}{x}+ frac{1}{x^3} }-1 } = frac{1}{-1}=-1")
В числителе 1/х² →0 и 1/х →0, в знаменателе 1/х→0 и 1/x³→0, поэтому в числителе остаётся √1, а в знаменателе -1. В итоге 1/-1=-1
Определяем "икс" в старшей степени и затем делим числитель и знаменатель на него.
(*)
В числителе 1/х² →0 и 1/х →0, в знаменателе 1/х→0 и 1/x³→0, поэтому в числителе остаётся √1, а в знаменателе -1. В итоге 1/-1=-1
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
9 лет назад