высота проведенная к основанию равнобедренного треугольника равна 8  см, а угол при основании равен 30 градусам. Найдите основаие треугольника 

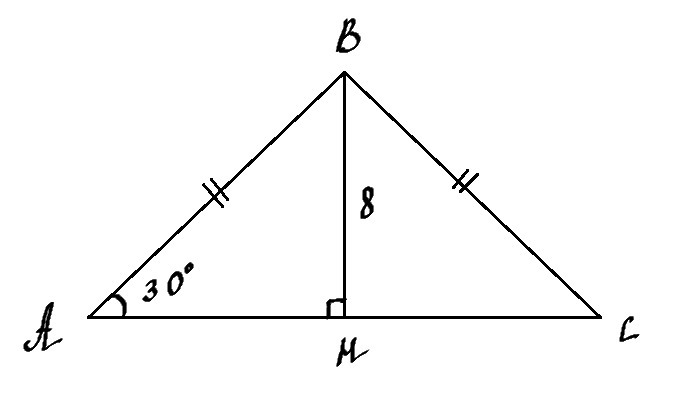
Рисунок к задаче в прикрепленном файле.

Рассмотрим ΔАВН. Он прямоугольный, т.к. ВН⊥АС.

В треугольнике ΔАВН ∠А = 30°, а лежащий напротив него катет ВН = 8 (по условию).

В прямоугольном треугольнике катет, лежащий напротив угла в 30° в два раза короче гипотенузы. Следовательно АВ = 2*ВН = 2*8 = 16 (см).

По теореме Пифагора

В равнобедренном треугольнике высота, проведенная из вершины, также является и медианой. Значит ВН - медиана и АН = НС =

АС = 2*АН = (см)

Ответ: АС = см