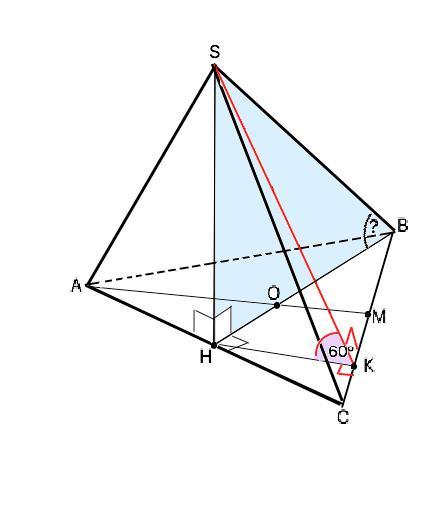
Основание пирамиды - правильный треугольник; Одна из боковых граней перпендикулярна к основанию, а две другие наклонены к нему под углом 60 градусов. Под каким углом наклонено к плоскости основания наибольшее боковое ребро?

Ответ: arctg√3/2

Подробное объяснение:

В пирамиде ЅАВС грань АЅС перпендикулярна основанию АВС. Грани АЅВ и СЅВ наклонены под равным углом к основанию, АВ=СВ (дано), ⇒ грани АЅВ и СЅВ равны, ⇒ АЅ=СЅ. Высота ЅН пирамиды ⊥АВС, следовательно,  ⊥ любой прямой в плоскости АВС.

Пусть АВ=ВС=АС= а.

 Высота ЅН -  медиана равнобедренного треугольника АЅС.⇒ АН=НС=а/2  Проекции ребер ЅА и ЅС равны половине стороны АС. Проекция ЅB=а√3/2 ⇒  ЅВ наибольшее ребро пирамиды, а угол ЅВН - искомый.

  Угол между основанием и боковой гранью –  двугранный. Его величина  определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.

  Проведем НК⊥ВС. Наклонная ЅК⊥ВС по т. о 3-х перпендикулярах. ∠ЅКН=60° (дано).

  Угол С в прямоугольном ∆ НКС=60°,  катет НК=НС•sin∠C=a2•√3/2=(a√3):4

 Из ∆ ЅНК высота ЅН=НК•tg60°=3a/4 ⇒

tg∠SBH=SH:BH=3a•2:4a√3=√3/2

Искомый угол =arctg√3/2