Ответы
Ответ дал:
0
Ответ: x=-1, x=1.
Ответ дал:
0
x^2=t
t^3+3t^2-t-3=0
3:+-1,+-3
t=1 1^3+3*1^2-1-3=0
t1=1 x1=-1 x2=1
деление на картинке
t^2+4t+3=0
d=16-12=4
t2=-3 (корень не действителен, т.к квадрат числа не может быть равен отрицательному числу)
t3=-1 (корень не действителен, т.к квадрат числа не может быть равен отрицательному числу)
Ответ: x1=1 x2=-1
t^3+3t^2-t-3=0
3:+-1,+-3
t=1 1^3+3*1^2-1-3=0
t1=1 x1=-1 x2=1
деление на картинке
t^2+4t+3=0
d=16-12=4
t2=-3 (корень не действителен, т.к квадрат числа не может быть равен отрицательному числу)
t3=-1 (корень не действителен, т.к квадрат числа не может быть равен отрицательному числу)
Ответ: x1=1 x2=-1
Приложения:
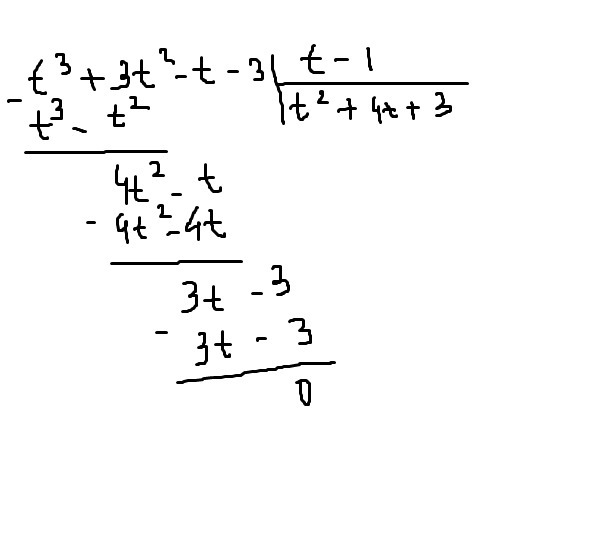
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад