помогите решить 3 и 4

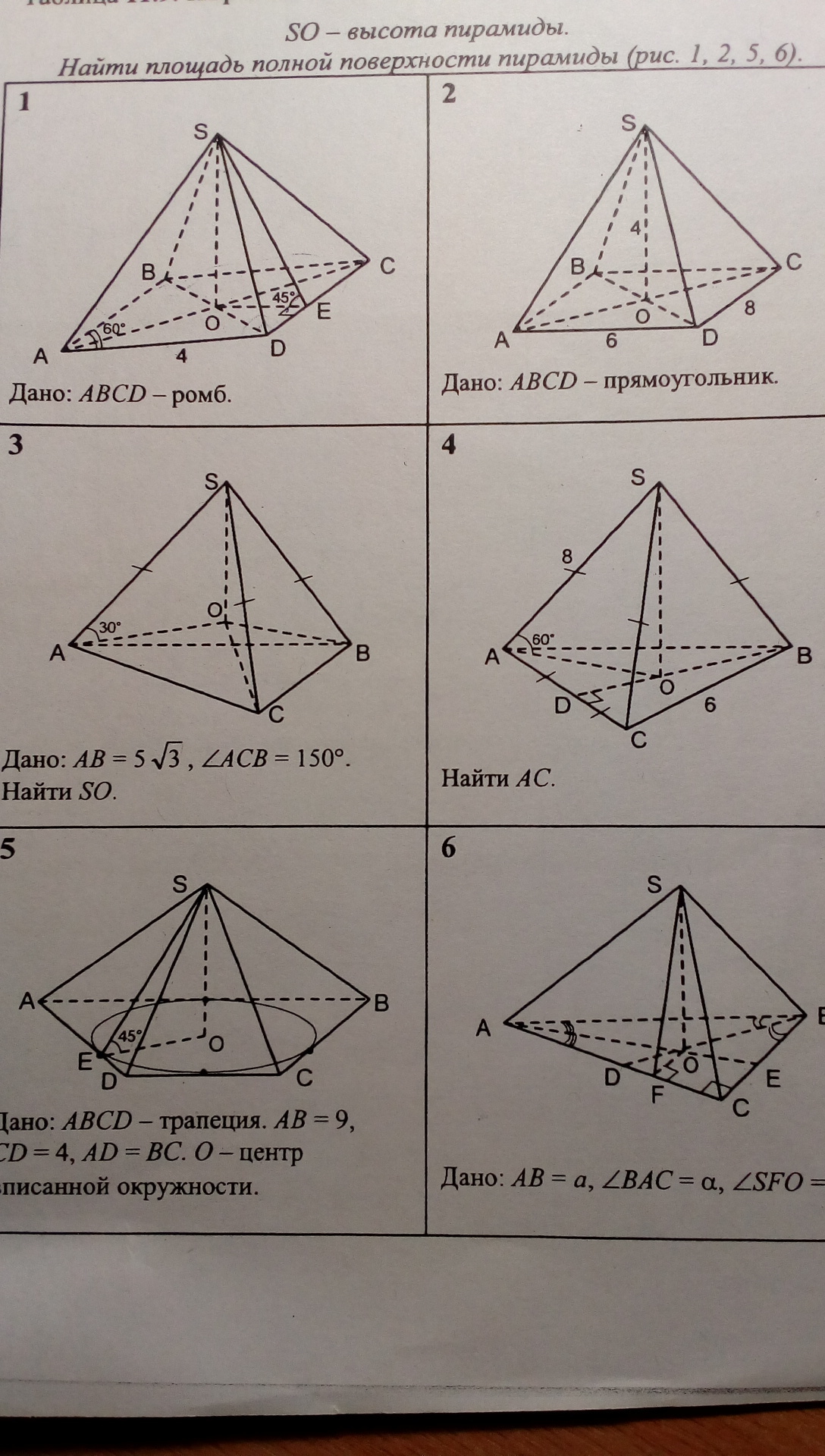
3) Если боковые рёбра равны, то вершины треугольника в основании пирамиды лежат на окружности.
Угол АСВ как вписанный равен половине центрального, который равен 150°*2 = 300°.
Остаток угла окружности - это угол АОВ и он равен 360°-300° = 60°.
Проекции рёбер на основание тоже равны (у них общая вертикальная высота SO).
Тогда равнобедренный треугольник АОВ с углом при вершине О в 60° является равносторонним: ОА = ОВ = АВ = 5√3 .
Из треугольника ASO находим SO = SА*tg30° = 5√3*(1/√3) = 5.