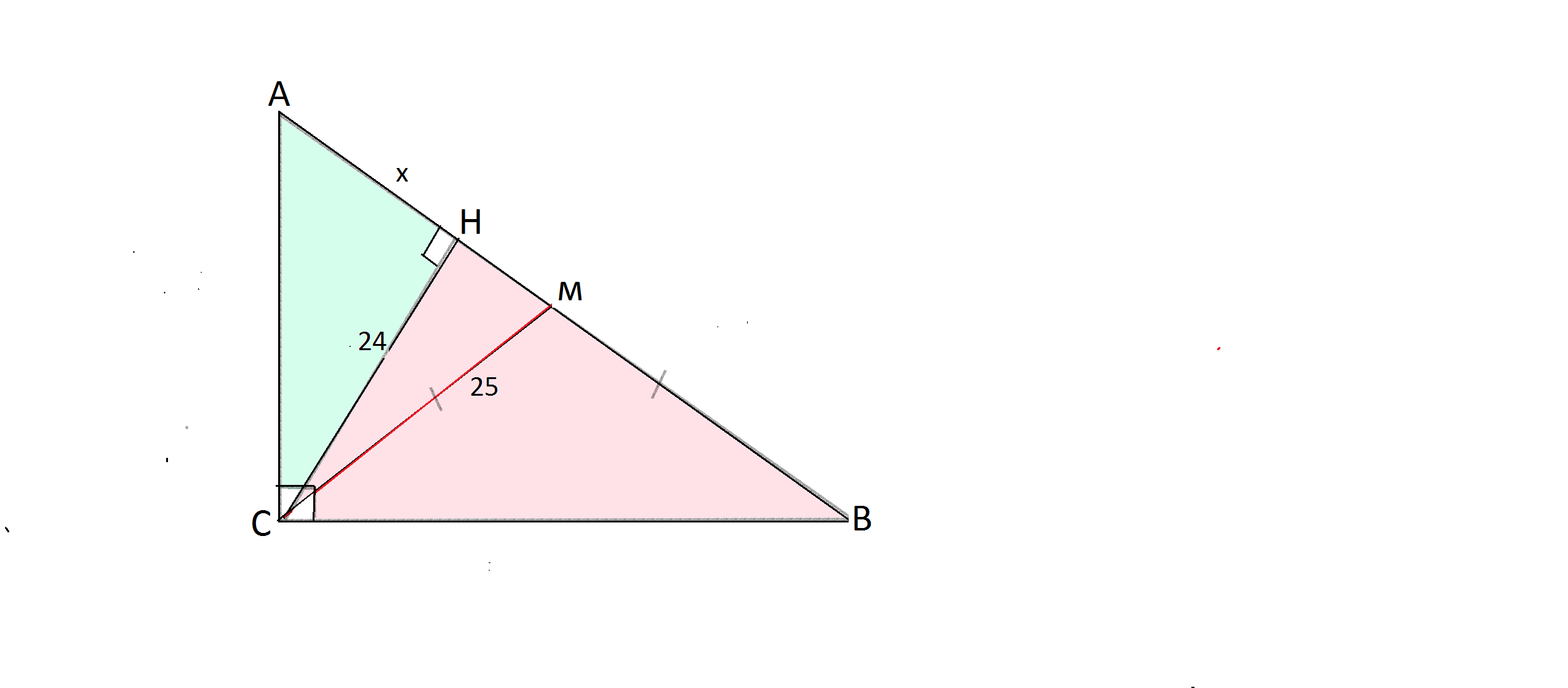
В прямоугольном треугольнике высота и медиана, проведенные к гипотенузе, равны 24 см и 25 см. Найдите периметр треугольника.
Ответы
Сделаем рисунок, обозначим вершины треугольника А, В, С, угол С=90°
Медиана прямоугольного треугольника равна половине гипотенузы (свойство), ⇒, гипотенуза АВ=2СМ=50 см
Высота СН делит треугольник на два треугольника, подобных друг другу и исходному (свойство).
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Пусть отрезок АН = х см, а НВ=50-х
Тогда: СН²=АН•НВ ⇒ 24²=х(50-х)
576=50х -х²
х²-50х+576=0
Решив квадратное уравнение, получим значения
х₁=18 и х₂=32
Из прямоугольных треугольников, на которые высота разбила исходный треугольник АВС, найдем длину катетов.
АС²=АН²+СН²
АС²=576+324=900 ⇒ АС=30 см
ВС²=СН²+НВ²
ВС²=576+1024=1600⇒ ВС=40
Откуда Р(АВС) =50+40+30=120 см
--------------------------------
В задачах часто встречаются прямоугольные треугольники, отношения сторон которых выражены целыми числами (так называемыми Пифагоровыми тройками)
Такие задачи нередко можно решить устно. Для этой задачи решение:
Медиана прямоугольного треугольника равна половине гипотенузы ( свойство). ⇒ АВ=2•СМ=50 см.
Высота СН⊥АВ Т.к. СН:СМ 24:25, катет МН=7 (из Пифагоровых троек 24:7:25)
Отрезок гипотенузы АН=АВ-(ВМ+МН)=50-(25+7)=18 см.
В ∆ СНА отношение катетов АН:СН=18:24=3:4 ⇒ k=24:4=6 ⇒ ∆ АСН египетский, СА=5•6=30 см
В ∆ АВС отношение АС:АВ=30:50=3:5 ⇒ ∆ АВС- египетский, k=АВ:5=50:5=10 ⇒ ВС=4•10=40 см
Р(АВС)=АВ+АС+АС=50+40+30=120 см