Предмет: Алгебра
Автор: DuramaKun
Вопрос задан 8 лет назад

Провести полное исследование и построить график указанной функции:
$y=x- frac{8}{ x^{4} }$

Ответы

Ответ дал: Аноним

1. Область определения функции:
Знаменатель не равно нулю, т.е. $xne 0$
$D(y)=(-infty;0)cup(0;+infty)$

2. Проверим на четность.
$y(-x)=-x- frac{8}{(-x)^4} =-(x+ frac{8}{x^4})ne y(x)$
Итак, функция ни четная ни нечетная.

3. Не периодическая функция.
4. Точки пересечения с осью Ох и Оу
4.1. С осью Ох(у=0):
$x- frac{8}{x^4}=0\ x^5=8\ x= sqrt[5]{8}$

4.2. С осью Оу(х=0):
$y=0- frac{8}{0^4}$
Точки пересечения с осью Оу нет.

5. Критические точки, возрастание и убывание функции:
Производная функции
$y'=(x- frac{8}{x^4})'=1+ frac{32}{x^5}$
Приравниваем производную функции к нулю
$1+ frac{32}{x^5} =0|cdot x^5\ x^5=-32\ x=-2$

___+__(-2)___-___(0)___+___
Функция возрастает на промежутке $(-infty;-2)$ и $(0;+infty)$ , а убывает на промежутке $xin (-2;0)$ . В точке x=-2 - имеет локальный максимум

6. Точка перегиба

$y''=(1+ frac{32}{x^5} )'=- frac{160}{x^6}$
очевидно, что нулей во второй производной нет, а значит точке перегиба нет.

Горизонтальных асимптот нет

Вертикальные асимптоты: $x=0$

Наклонные асимптоты: $lim_{x to infty} (x- frac{8}{x^4} -x)=0$
Тоесть наклонная асимптота $y=x$

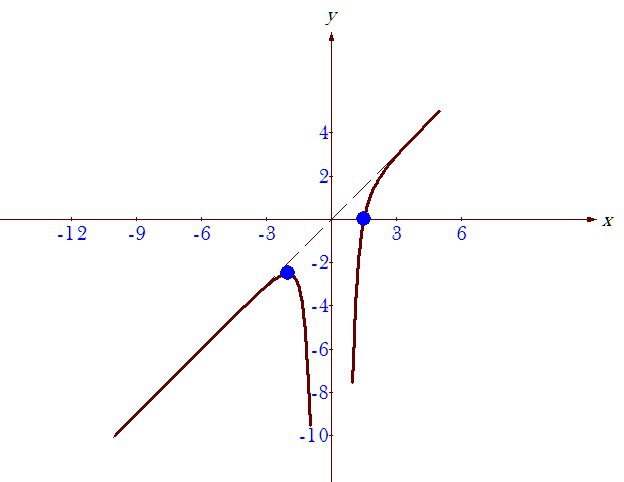
Строим график

Приложения: