Основание прямой призмы прямоугольный треугольник с гипотенузой 10 см и катетом 6 см. Больший катет треугольника в основании призмы равен диагонали меньшей из боковых граней. Найти высоту призмы.
Можно решение выслать фотографией с рисунком и решением

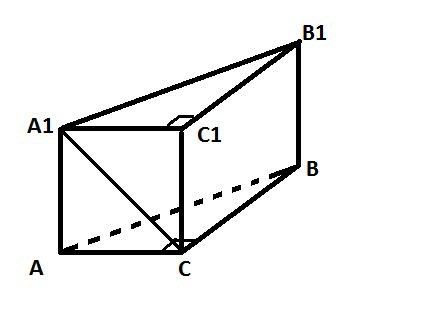
Пусть ABCA1B1C1 - прямая призма, её основания - прямоугольные треугольники ABC и A1B1C1 с прямыми углами C и C1 соответственно. Катет основания AC = 6 см. (см. рис.).
Все боковые грани имеют одинаковую высоту. Значит, меньшая боковая грань та, у которой меньше ширина. Это грань AA1C1C.
По т. Пифагора 

По условию задачи A1C = BC = 8 см.
Тогда, из тр-ка AA1C по т. Пифагора высота призмы AA1