Найдите площадь треугольника, вершинами которого являются точки персечения прямых х=1 , у=-2 , у= -2х+6

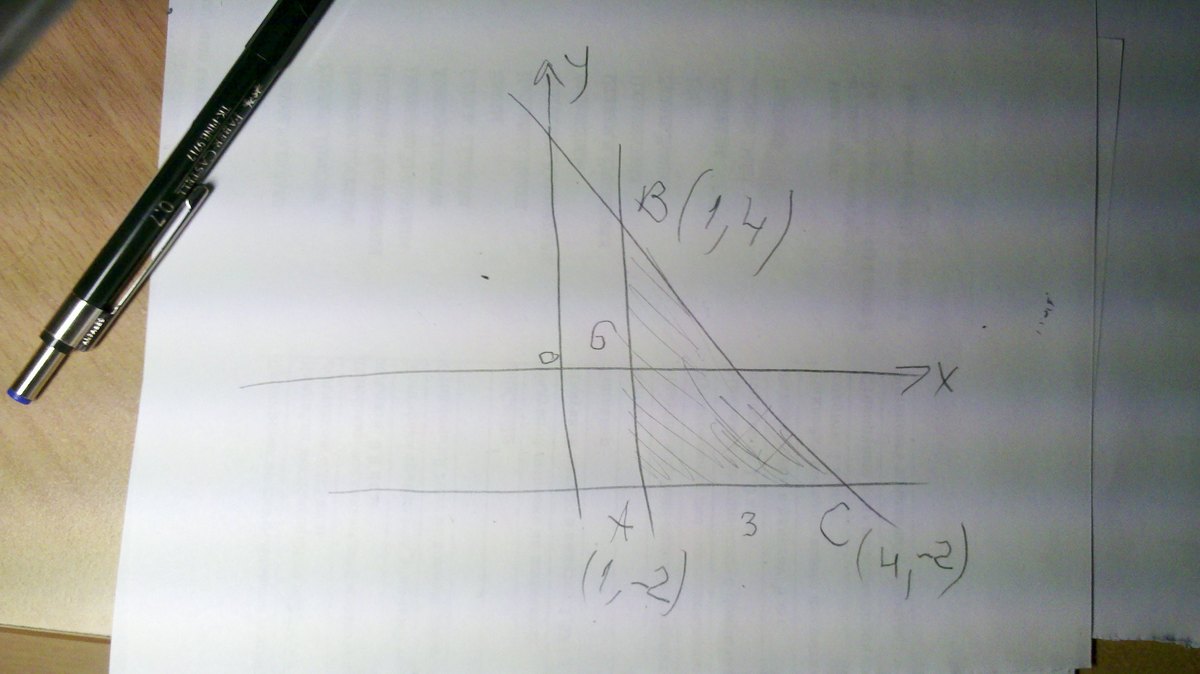
Прямые х=1 и у=-2 пересекаются в точке с координатами (1,-2) Это будет точка А.

Прямая х=1 и прямая у=-2х+6 пересекаются в точке с координатами х=1 у=-2*1+6+=4, т.е. (1,4) Это будет точка В.

Прямая у=-2 и прямая у=-2х+6 пересекаются в точке с координатами у=-2, а х находим из уравнения

-2=-2х+6, х=4 Координаты (4,-2) Это будет точка С.

Получился прямоугольный треугольник. Катет АВ - вертикальный его длина разность координат у у точек А и В: 4-(-2)=6, катет АС - горизонтальный, его длина разность координат х у точек А и С: 4-1=3

Площадь треугольника 6*3/2=9