Площадь сечения куба плоскостью, проходящей через диагонали верхнего и нижнего оснований равна 16 корней из 2 . Найдите ребро куба

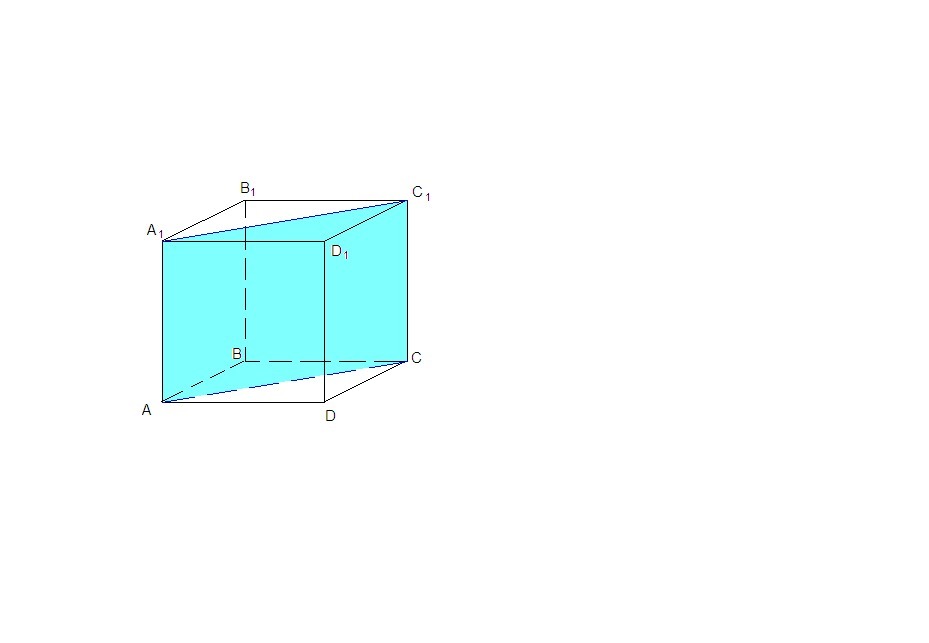
АА₁С₁С - сечение, проходящее через диагонали верхнего и нижнего оснований.
Боковые ребра АА₁ и СС₁ равны и параллельны, они перпендикулярны плоскости основания, значит сечение - прямоугольник.

Пусть ребро куба  - а.
Тогда АС = А₁С₁ = а√2 как диагональ квадрата.

Saa₁c₁c = AC · AA₁
a√2 · a = 16√2
a² = 16
a = 4