Один из углов прямоугольного треугольника равен 49 градусов. Найдите угол между биссектрисой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах. Если можно начертите чертёж.

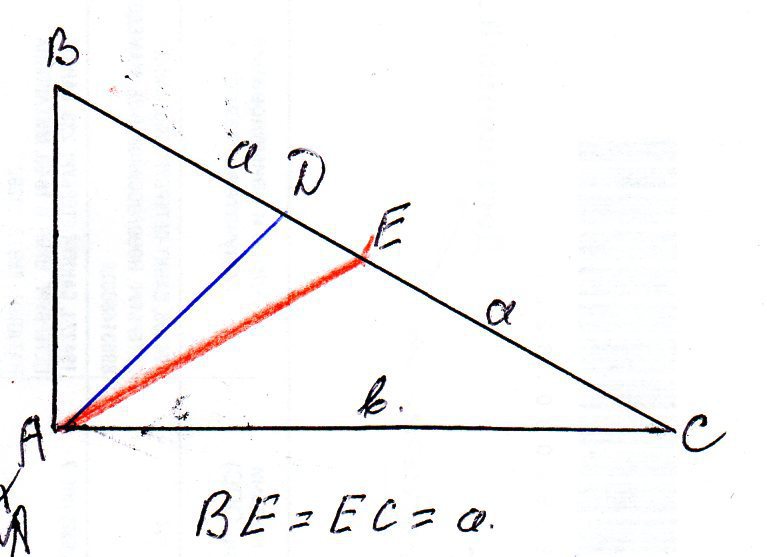
АЕ-медианна, ВЕ=ЕС=а   АД-биссектриса   Угол ДАС=ДАВ=45 градусам
b/2a=cos39           b=2acos39
AE²=a²+b²-2abcos39        AE²=a²+4a²cos²39-4a²cos²39
AE²=a²    AE=a  треугольник АЕС равнобедренний ⇒угол ЕАС=39
тогда ДАЕ=45-39=6 градусов

Ответ неправильный