стороны прямоугольника раны 10и 24 .найдите радиус окружности,описанной около этого прямоугольника

Радиус окружности - половина диагонали. Диагональ ищестся по теореме Пифагора, d=sqrt(10^2+24^2)=26

R=13

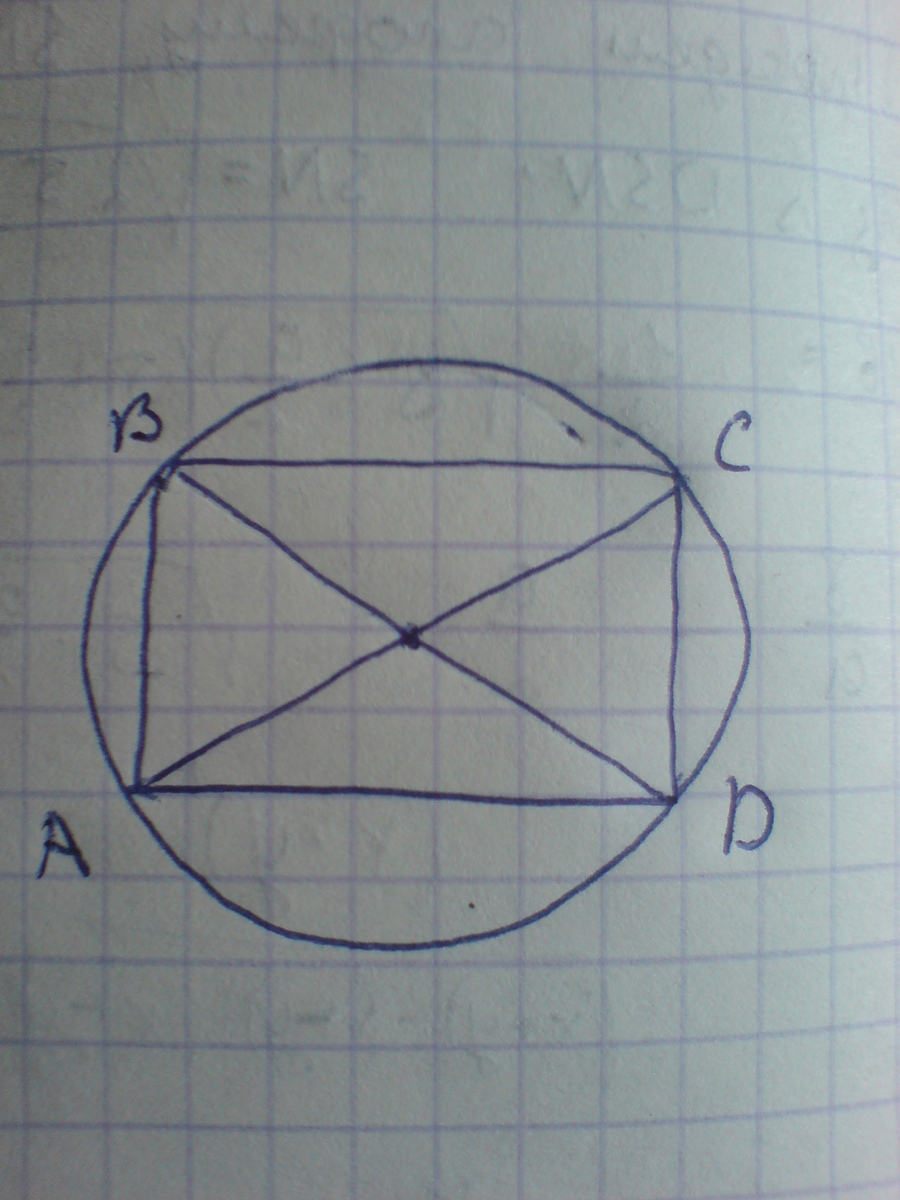
Во вложении видно,что диогональ(BD) прямоугольника это диаметр круга. А радиус круга равен половине диаметра.R=BD/2.Сначало находим диогональ(BD):

R=BD/2=26/2=13

Ответ: R=13