В окружность радиуса 10 см вписали квадрат ABCD.Найдите площадь кольца,ограниченного данной и вписанной в квадрат окружности помогите плиз
Ответы
Ответ дал:
0
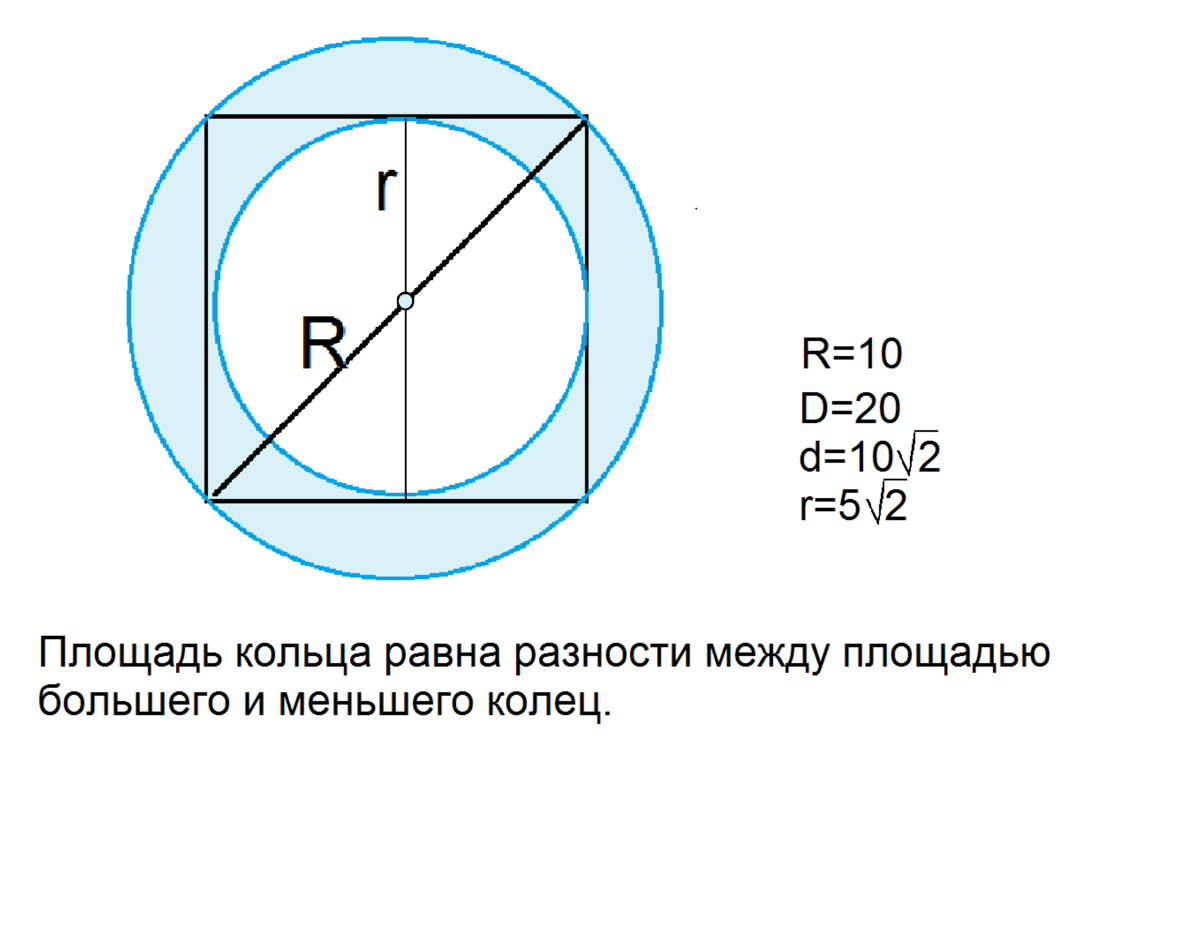
Искомая площадь - разность между площадью большего и меньшего кругов, ограниченных описанной вокруг квадрата и вписанной в квадрат окружностей .
Диаметр описанной окружности является диагональю квадрата.
Из формулы D=a√2
найдем а ( сторону квадрата)
а=D:√2
D=2R=20
a=20:√2 =10√2
Радиус вписанной в квадрат окружности равен половине стороны квадрата.
r=5 √2
S (1)=π R²=100π
S(2)=πr²=50π
S кольца=100π-50π=50π
———
[email protected]
Приложения:
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад