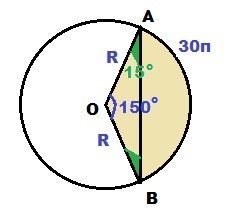
длина дуги стягиваемой хордой равна 30 пи см а угол образованный этой хордой и радиусом проведённым через его конец равен 15 градусов. найдите площадь сектора ограниченного этой дугой.

ΔOAB образован двумя радиусами R и хордой ⇒ равнобедренный
∠OBA = ∠OAB = 15°   ⇒   ∠AOB = 180°-2*15° = 150°
∠AOB = 150° - центральный   ⇒  дуга AB = 150°
Длина дуги 
  см

Площадь сектора
 

Ответ: площадь сектора 540π см²