биссектрисы углов А иВ параллелограмма АВСД пересекаются в точке К. докажите что окружность с диаметром АВ проходит через К

ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО!! ЗАРАНЕЕ СПАСИБО!

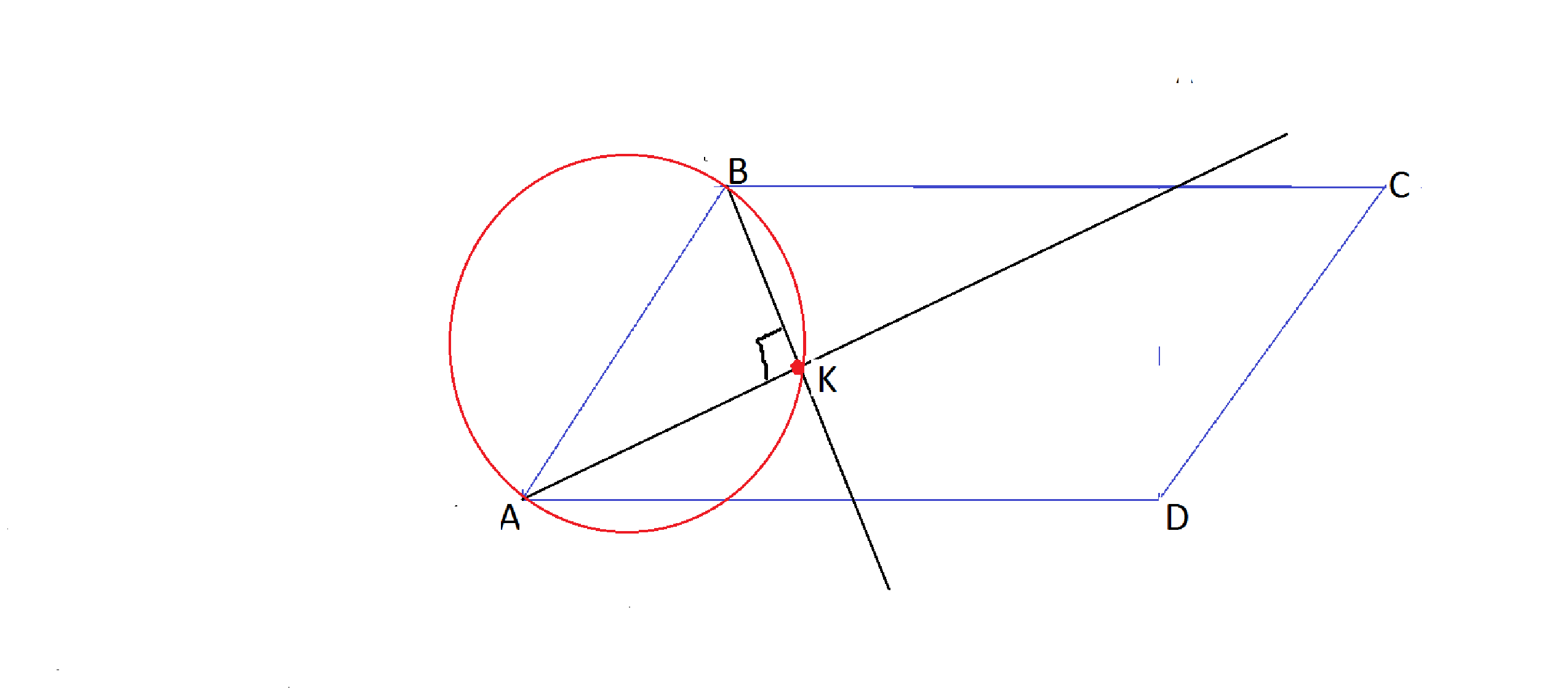
Сторона параллелограмма АВ и отрезки биссектрис до их пересечения образуют треугольник АВК.
Так как сумма углов при одной стороне параллелограмма равна 180 градусов,

сумма их половин будет вдвое меньше - 90 градусов.
На угол, образовавшийся при пересечении биссектрис, остается 90 градусов. Треугольник АВК - прямоугольный.
Если его гипотенуза - диаметр окружности,
то вершина, содержащая прямой угол, лежит на окружности, так как

прямоугольный треугольник АВК в этом случае - вписанный.