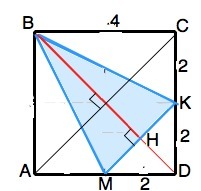
сторона квадрата равна 4. Если соединить середины двух смежных сторон и противоположную вершину квадрата , то площадь полученного треугольника равна

 Задачу можно решать разными способами. Рассмотрим  один из них.

 Диагонали квадрата равны, взаимно перпендикулярны, делят его углы на два по 45°.  ВD=АС=АВ:sin45°.   АС=(4:√2)/2=4√2 см  

Как  средняя линия  ∆ АСD,  МК=АС:2=2√2 см.  ВD⊥АС ⇒  ВН⊥МК  ( по свойству перпендикуляра, проведенного к одной из параллельных прямых) и является высотой ∆ МВК.   ВН=ВD-HD. НD– медиана прямоугольного ∆ МDK и равна половине его гипотенузы. HD=МК:2=√2. ⇒ ВН=4√2-√2=3√2.

Площадь  ∆(МВК)=ВН•МК:2. S(МВК)=(3√2•2√2):2=6 см²