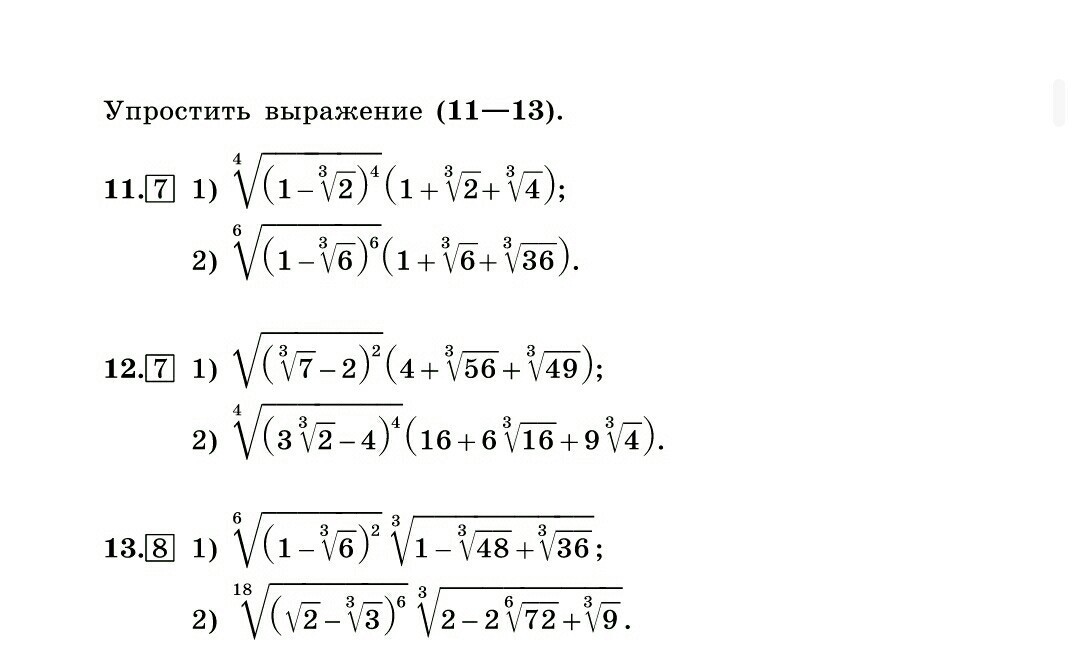Ответы
Ответ дал:
0
11
1)![sqrt[4]{(1- sqrt[3]{2} )^4} =|1- sqrt[3]{2} |= sqrt[3]{2} -1](https://tex.z-dn.net/?f=+sqrt%5B4%5D%7B%281-+sqrt%5B3%5D%7B2%7D+%29%5E4%7D+%3D%7C1-+sqrt%5B3%5D%7B2%7D+%7C%3D+sqrt%5B3%5D%7B2%7D+-1 "sqrt[4]{(1- sqrt[3]{2} )^4} =|1- sqrt[3]{2} |= sqrt[3]{2} -1")
(∛2-1)(1+∛2+∛4)=(∛2)³-1³=2-1=1
2)![sqrt[6]{(1- sqrt[3]{6})^6 } =|1- sqrt[3]{6} |= sqrt[3]{6} -1](https://tex.z-dn.net/?f=+sqrt%5B6%5D%7B%281-+sqrt%5B3%5D%7B6%7D%29%5E6+%7D+%3D%7C1-+sqrt%5B3%5D%7B6%7D+%7C%3D+sqrt%5B3%5D%7B6%7D+-1 "sqrt[6]{(1- sqrt[3]{6})^6 } =|1- sqrt[3]{6} |= sqrt[3]{6} -1")
(∛6-1)(1+∛6)+∛36)=(∛6)³-1³=6-1=5
12
1)![sqrt{( sqrt[3]{7} -2)^2} =| sqrt[3]{7} -2|=2- sqrt[3]{7}](https://tex.z-dn.net/?f=+sqrt%7B%28+sqrt%5B3%5D%7B7%7D+-2%29%5E2%7D+%3D%7C+sqrt%5B3%5D%7B7%7D+-2%7C%3D2-+sqrt%5B3%5D%7B7%7D+ "sqrt{( sqrt[3]{7} -2)^2} =| sqrt[3]{7} -2|=2- sqrt[3]{7}")
(2-∛7)(4+∛56+∛49)=2³(∛7)³=8-7=1
2)![sqrt[4]{(3 sqrt[3]{2} -4)^4} =|3 sqrt[3]{2} -4|=4-3 sqrt[3]{2}](https://tex.z-dn.net/?f=+sqrt%5B4%5D%7B%283+sqrt%5B3%5D%7B2%7D+-4%29%5E4%7D+%3D%7C3+sqrt%5B3%5D%7B2%7D+-4%7C%3D4-3+sqrt%5B3%5D%7B2%7D+ "sqrt[4]{(3 sqrt[3]{2} -4)^4} =|3 sqrt[3]{2} -4|=4-3 sqrt[3]{2}")
(4-3∛2)(16+6∛16+9∛4)=4³-(3∛2)²=64-54=10
13
![1) sqrt[3]{( sqrt[3]{6}-1 )(sqrt[3]{6}-1)^2 } =[tex] sqrt[3]{( sqrt[3]{6} -1)^3} =](https://tex.z-dn.net/?f=1%29+sqrt%5B3%5D%7B%28+sqrt%5B3%5D%7B6%7D-1+%29%28sqrt%5B3%5D%7B6%7D-1%29%5E2+%7D+%3D%5Btex%5D+sqrt%5B3%5D%7B%28+sqrt%5B3%5D%7B6%7D+-1%29%5E3%7D+%3D "1) sqrt[3]{( sqrt[3]{6}-1 )(sqrt[3]{6}-1)^2 } =[tex] sqrt[3]{( sqrt[3]{6} -1)^3} =")
sqrt[3]{6} [/tex]-1
-----------------------------
![sqrt[6]{(1- sqrt[3]{6} )^2} = [tex] sqrt[6]{( sqrt[3]{6}-1)^2 } = sqrt[3]{6} -1](https://tex.z-dn.net/?f=+sqrt%5B6%5D%7B%281-+sqrt%5B3%5D%7B6%7D+%29%5E2%7D+%3D+%5Btex%5D+sqrt%5B6%5D%7B%28+sqrt%5B3%5D%7B6%7D-1%29%5E2+%7D+%3D+sqrt%5B3%5D%7B6%7D+-1 "sqrt[6]{(1- sqrt[3]{6} )^2} = [tex] sqrt[6]{( sqrt[3]{6}-1)^2 } = sqrt[3]{6} -1")
![2)[tex] sqrt[3]{( sqrt[3]{3} -sqrt{2} )( sqrt[3]{3} - sqrt{2} )^2 } = sqrt[3]{( sqrt[3]{3} - sqrt{2})^3 } = sqrt[3]{3} - sqrt{2}](https://tex.z-dn.net/?f=2%29%5Btex%5D+sqrt%5B3%5D%7B%28+sqrt%5B3%5D%7B3%7D+-sqrt%7B2%7D+%29%28+sqrt%5B3%5D%7B3%7D+-+sqrt%7B2%7D+%29%5E2+%7D+%3D+sqrt%5B3%5D%7B%28+sqrt%5B3%5D%7B3%7D+-+sqrt%7B2%7D%29%5E3+%7D+%3D+sqrt%5B3%5D%7B3%7D+-+sqrt%7B2%7D+ "2)[tex] sqrt[3]{( sqrt[3]{3} -sqrt{2} )( sqrt[3]{3} - sqrt{2} )^2 } = sqrt[3]{( sqrt[3]{3} - sqrt{2})^3 } = sqrt[3]{3} - sqrt{2}")
-----------------------------------
![sqrt[18]{( sqrt{2} - sqrt[3]{3} )^6} =[tex] sqrt[18]{( sqrt[3]{3}- sqrt{2} )^6} = sqrt[3]{ sqrt[3]{3} - sqrt{2} }](https://tex.z-dn.net/?f=+sqrt%5B18%5D%7B%28+sqrt%7B2%7D+-+sqrt%5B3%5D%7B3%7D+%29%5E6%7D+%3D%5Btex%5D+sqrt%5B18%5D%7B%28+sqrt%5B3%5D%7B3%7D-+sqrt%7B2%7D+%29%5E6%7D+%3D+sqrt%5B3%5D%7B+sqrt%5B3%5D%7B3%7D+-+sqrt%7B2%7D+%7D+ "sqrt[18]{( sqrt{2} - sqrt[3]{3} )^6} =[tex] sqrt[18]{( sqrt[3]{3}- sqrt{2} )^6} = sqrt[3]{ sqrt[3]{3} - sqrt{2} }")
1)
(∛2-1)(1+∛2+∛4)=(∛2)³-1³=2-1=1
2)
(∛6-1)(1+∛6)+∛36)=(∛6)³-1³=6-1=5
12
1)
(2-∛7)(4+∛56+∛49)=2³(∛7)³=8-7=1
2)
(4-3∛2)(16+6∛16+9∛4)=4³-(3∛2)²=64-54=10
13
-----------------------------
-----------------------------------
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад