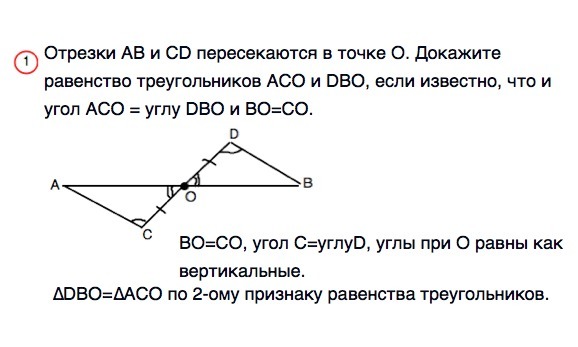
1, Отрезки AB и CD пересекаются в точке О. Докажите равенство треугольников ACO и DBO, если известно, что и угол ACO = углу DBO и BO=CO.

2, Развёрнутый угол ABC разделен лучом на два луча, один из которых на 34 градуса больше другого. Найдите образовавшиеся углы.

3, Точка М пренадлежит отрезку АВ. МВ на 4,5 дм больше чем АМ. Найдите длину отрезков АМ и МВ, если АВ=11,3дм