Четырёхугольник ABCD-трапеция. Найди ее площадь,сделав необходимые измерения

Приложения:

Ответы

Ответ дал: Аноним

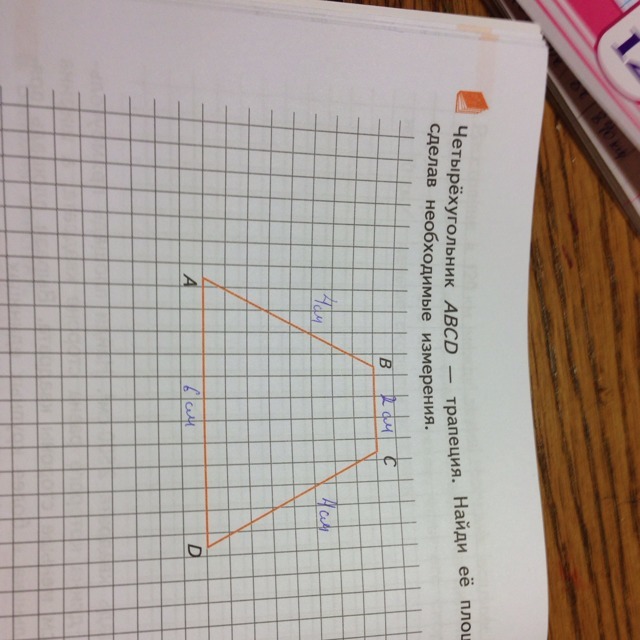
Из вершины угла С проведем перпендикуляр к стороне основания АD; CH - высота трапеции. Поскольку AB = CD, то трапеция ABCD - равнобедренная

$tt HD=dfrac{AD-BC}{2}=dfrac{6-2}{2}=2$ см.

Из прямоугольного треугольника CHD найдем CH по т. Пифагора

$tt CH=sqrt{CD^2-HD^2}=sqrt{4^2-2^2}=sqrt{16-4}=sqrt{12}=2sqrt{3}$ см

Площадь трапеции: $tt S=dfrac{AD+BC}{2}cdot CH=dfrac{6+2}{2}cdot2sqrt{3}=8sqrt{3}$ см²

Приложения:

Похожие вопросы

Русский язык

2 года назад

Окружающий мир

2 года назад

История

6 лет назад

Математика

6 лет назад

Математика

9 лет назад

Литература

9 лет назад

Алгебра

9 лет назад

История

9 лет назад