Радиус основания конуса равен 6см, его высота 12см, Найдите площадь сечения, проведённого параллельно оси конуса на расстоянии 2см от неё.

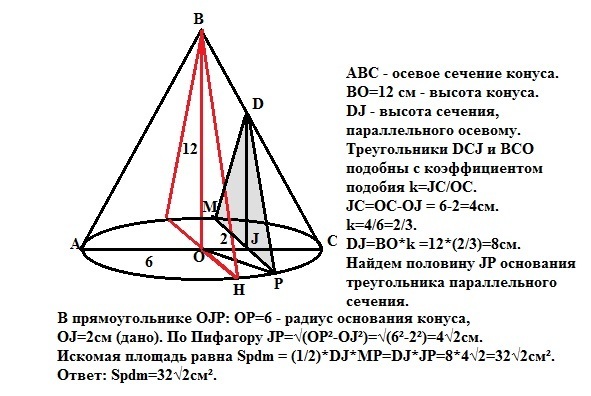
ABC - осевое сечение конуса.
ВО=12 см - высота конуса.
DJ - высота сечения, параллельного осевому.
Треугольники DСJ и ВСО  подобны с коэффициентом подобия k=JC/OC.
JС=OС-OJ = 6-2=4см.
k=4/6=2/3.
DJ=BO*k =12*(2/3)=8см.
Найдем половину JP основания треугольника параллельного сечения.
В прямоугольнике OJP: OР=6 - радиус основания конуса,
OJ=2см (дано). По Пифагору JP=√(OP²-OJ²)=√(6²-2²)=4√2см.
Искомая площадь равна Spdm = (1/2)*DJ*МP=DJ*JP=8*4√2=32√2см².
Ответ: Spdm=32√2см².