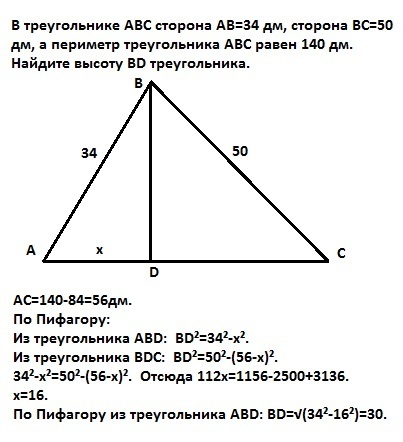
В треугольнике ABC сторона AB=34 дм, сторона BC=50 дм, а периметр треугольника ABC равен 140 дм. Найдите высоту BD треугольника.
Ответы
Ответ дал:
0
Сторона АС равна 140-34-50=56дм.
Найдем площадь треугольника АВС по Герону:
S=√[p(p-a)(p-b)(p-c)], где р - полупериметр, a,b,c - стороны треугольника.
В нашем случае S=√(70*36*20*14)=√(14*100*36*14)=840дм².
С другой стороны, Sabc=(1/2)*BD*AC, отсюда
BD=2S/АС или BD=2*840/56=30дм.
Ответ: BD=30дм.
Вариант решения по Пифагору:
АС=140-84=56дм.
По Пифагору:
Из треугольника АВD: BD²=34²-x².
Из треугольника ВDC: BD²=50²-(56-x)².
34²-x²=50²-(56-x)². Отсюда 112х=1156-2500+3136.
х=16.
По Пифагору из треугольника АВD: BD=√(34²-16²)=30.
Ответ: BD=30дм.
Найдем площадь треугольника АВС по Герону:
S=√[p(p-a)(p-b)(p-c)], где р - полупериметр, a,b,c - стороны треугольника.
В нашем случае S=√(70*36*20*14)=√(14*100*36*14)=840дм².
С другой стороны, Sabc=(1/2)*BD*AC, отсюда
BD=2S/АС или BD=2*840/56=30дм.
Ответ: BD=30дм.
Вариант решения по Пифагору:
АС=140-84=56дм.
По Пифагору:
Из треугольника АВD: BD²=34²-x².
Из треугольника ВDC: BD²=50²-(56-x)².
34²-x²=50²-(56-x)². Отсюда 112х=1156-2500+3136.
х=16.
По Пифагору из треугольника АВD: BD=√(34²-16²)=30.
Ответ: BD=30дм.
Приложения:
Ответ дал:
0
а по теореме Пифагора?
Ответ дал:
0
АС=140-84=56дм.
По Пифагору:
Из треугольника АВD: BD²=34²-x².
Из треугольника ВDC: BD²=50²-(56-x)².
34²-x²=50²-(56-x)². Отсюда 112х=1156-2500+3136.
х=16.
По Пифагору из треугольника АВD: BD=√(34²-16²)=30.
Ответ: BD=30дм.
По Пифагору:
Из треугольника АВD: BD²=34²-x².
Из треугольника ВDC: BD²=50²-(56-x)².
34²-x²=50²-(56-x)². Отсюда 112х=1156-2500+3136.
х=16.
По Пифагору из треугольника АВD: BD=√(34²-16²)=30.
Ответ: BD=30дм.
Ответ дал:
0
Извините, так по теореме Пифагора можно? А то комментарии удалены..
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад