Предмет: Математика
Автор: troeshnik1881
Вопрос задан 8 лет назад

< >

Ребят, помогите с заданием пожалуйста.

Найдите площадь фигуры, ограниченной линиями $y= x^{3}-3x^{2}-9x+1;$ $x=0;$ $y=6;$ $x textless 0;$

Желательно с объяснениями, за ранее спасибо)

Ответы

Ответ дал: arsenlevadniy

0

$y= x^{3}-3x^{2}-9x+1; x=0; y=6, x textless 0. \ x^{3}-3x^{2}-9x+1=6, x textless 0, \ x^{3}-3x^{2}-9x-5=0, \ x_1=-1. \ x_2=0. \ intlimits_{-1}^0 {(6-(x^{3}-3x^{2}-9x+1))} , dx = intlimits_{-1}^0 {(-x^{3}+3x^{2}+9x+5)} , dx = \ =(-frac{x^4}{4}+x^3+frac{9x^2}{2}+5x)|_{-1}^0 =\=-(-frac{(-1)^4}{4}+(-1)^3+frac{9cdot(-1)^2}{2}+5cdot(-1)) =0,25+1-4,5+5=2,15.$

Приложения:

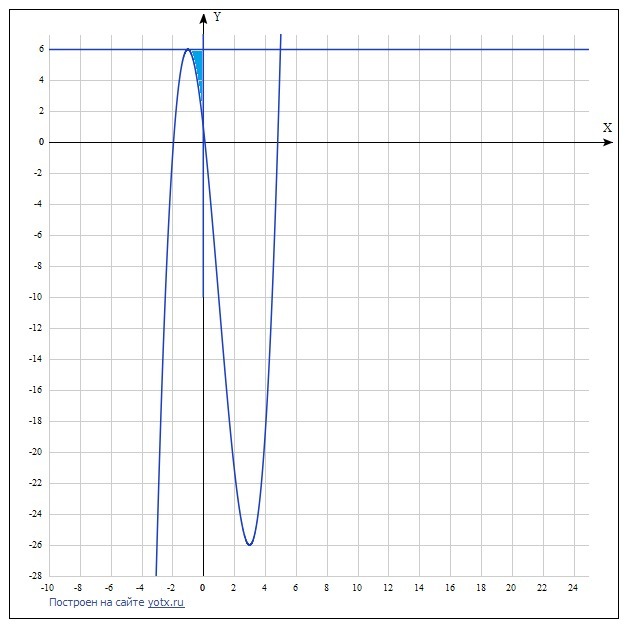
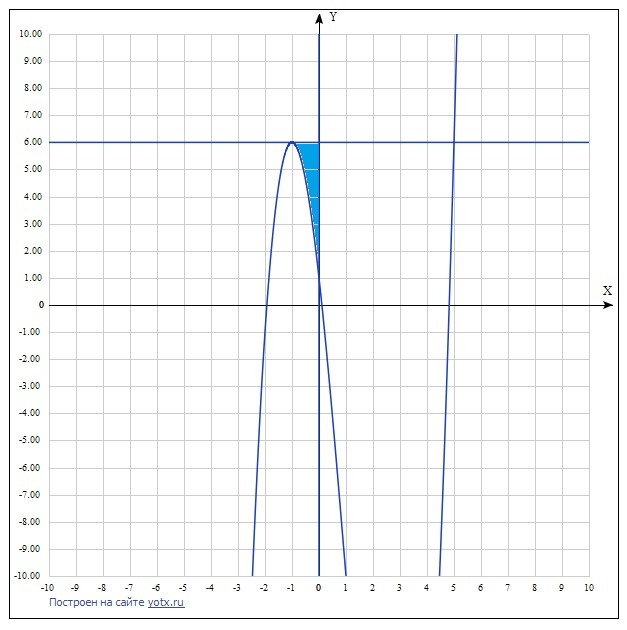
Ответ дал: troeshnik1881

0

А еще такой вопрос, как получилось x=-1 ; x=0 ?

Ответ дал: arsenlevadniy

0

x=0 по условию

Ответ дал: troeshnik1881

0

а -1?

Ответ дал: arsenlevadniy

0

х=-1 - корень уравнения подбором среди делителей 5, по условию х<0.

Ответ дал: troeshnik1881

0

Если есть время, гляньте вот это еще https://znanija.com/task/22117917

Похожие вопросы

Английский язык

2 года назад

СРОЧНО Помогите с англ, пожалуйста, замучилась составлять к вопрос( сформулируйте вопрос к выделенным словам 1. most people need MORE money than they have currently available 2. in general,

Русский язык

2 года назад

Какие правила написания букв гласных и Ь с буквами шипящих звуков здесь показаны? Напиши и назови каждую группу. Шишка, щупальца, ночка, ночь, лещ, жить, ножища, борщ, помощь, гречневая, стриж,

Математика

6 лет назад

Найди отношение указанных чисел. 36/49 к 6/35

Алгебра

6 лет назад

помогите пожалуйста за 8 класс!!!!!!!!!

Литература

9 лет назад

Выполни деление и Сделай проверку 185:56 450:73 204:17 312:24 759:23 544:17 962:26 825:33

Алгебра

9 лет назад

Составь равенство, соответствующее данному утверждению: Чтобы найти число b, составляющее 25%от числа a, надо умножить число a на 25 и разделить полученное произведение на 100.

Математика

9 лет назад

бабушка посадила 20 луковиц тюльпанов а внучка 4 раза меньше после этого у них осталось 10 луковиц сколько луковиц тюльпанов у них было сначала?

Математика

9 лет назад

вычислите наиболее рациональным способом а)2,7+7,8-3,7+1,2= б)0,2*(-9,83)*50=