Образующая конуса составляет с плоскостью его основания угол в 30, а радиус основания конуса равен 6 см. Найдите площадь полной поверхности конуса.

Считаем, что конус прямой ))

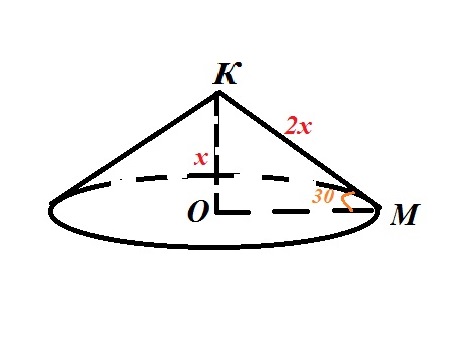
Рассмотрим осевое сечение конуса плоскостью. В сечении - равнобедренный треугольник.

Образуется прямоугольный треугольник КОМ с углом 30*. Тогда гипотенуза КМ в 2 раза больше катета КО=х.

По теореме Пифагора в треугольнике КОМ:

Н=KO= , L=KM=

Площадь полной пов-ти конуса: