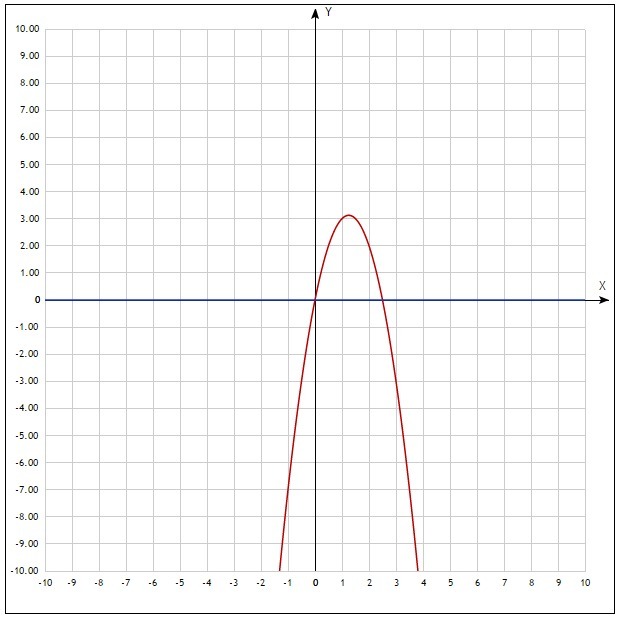
Найдите плащадь фигуры предварительно построив график ограниченной линиями y=5x-2xв квадрате и y=0
Ответы
Ответ дал:
0
График во вложении (красный  , синий
, синий  )
)
Найдем границы интегрирования:

Теперь решаем определенный интеграл:

Ответ: Площадь фигуры ограниченной линиями и
и  , равна
, равна  ед².
ед².
Найдем границы интегрирования:
Теперь решаем определенный интеграл:
Ответ: Площадь фигуры ограниченной линиями
Приложения:
Похожие вопросы
2 года назад
6 лет назад
9 лет назад
9 лет назад