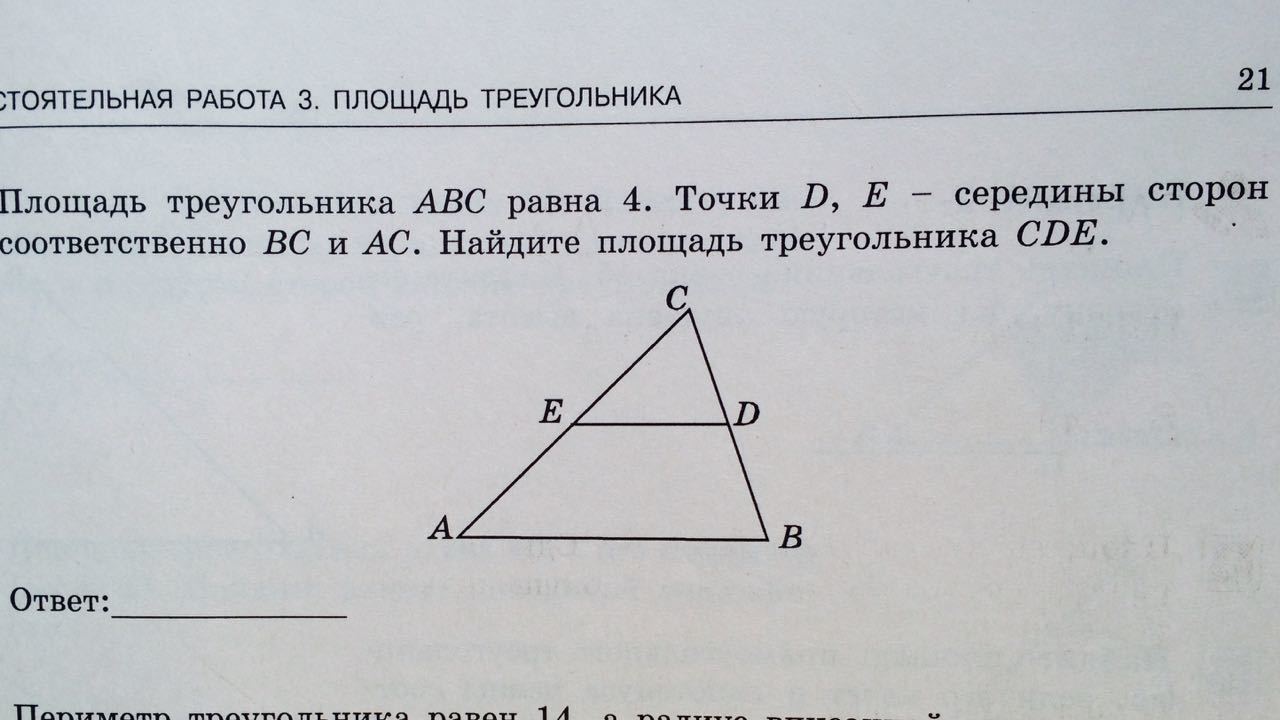
Площадь треугольника ABC равна 4. Точки D, E - середины сторон соответственно BC и AC. Найдите площадь треугольника CDE.

ED - средняя линия треугольника ABC, и поэтому ED=0,5AB
ΔABC~ΔCDE (т.к ∠CAB=∠CED и ∠CBA=∠CDE)
Отсюда следует, что Sabc~Sced ⇒
Sabc/Sced=AB/ED                                                        Sced=Sabc*ED/AB=Sabc*0,5AB/Ab=0,5Sabc=0,5*4=2

Ответ:

1 кв.ед.

Объяснение:

Воспользуемся заданным рисунком . Так как точки D и  E  - середины сторон BC и AC соответственно, то  DE - средняя линия . По свойству средней линии DE║ АВ и DE= 0,5 АВ.

Δ ECD подобен Δ ACB по двум углам ( ∠С - общий, ∠CED = ∠CAB, как накрест лежащие образованные  DE║ АВ и секущей АС.) Коэффициент подобия равен отношению соответственных сторон:

.

Площади подобных фигур относятся с  k², т.е.

Значит

кв. ед.