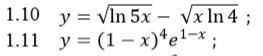Ответы
Ответ дал:
0
1.10
применим формулу производной корня ( √х)' = 1/(2√х) и учтём, что под корнем стоит сложная функция.
y' = 1/(2√ln5x) * (ln5x)' - 1/(2√x*ln4) * (x*ln4)' =
=1/(2√ln5x) * 1/5x * (5x)' -1/(2√x*ln4) * ln4 =
= 1/(2√ln5x) * 1/5x *5 - ln4/(2√x*ln4)= 1/(2√ln5x) * 1/x - ln4/(2√x*ln4)
1.11
применим формулу (UV)' = U'V + UV' и учтём, что каждый множитель - сложная функция.
y' = 4(1-x)³ * (1-x)' * e^(1-x) + (1-x)⁴ * e^(1-x) * (1-x)' =
=- 4(1-x)³ *e^(1-x) - (1-x)⁴ * e^(1-x)
применим формулу производной корня ( √х)' = 1/(2√х) и учтём, что под корнем стоит сложная функция.
y' = 1/(2√ln5x) * (ln5x)' - 1/(2√x*ln4) * (x*ln4)' =
=1/(2√ln5x) * 1/5x * (5x)' -1/(2√x*ln4) * ln4 =
= 1/(2√ln5x) * 1/5x *5 - ln4/(2√x*ln4)= 1/(2√ln5x) * 1/x - ln4/(2√x*ln4)
1.11
применим формулу (UV)' = U'V + UV' и учтём, что каждый множитель - сложная функция.
y' = 4(1-x)³ * (1-x)' * e^(1-x) + (1-x)⁴ * e^(1-x) * (1-x)' =
=- 4(1-x)³ *e^(1-x) - (1-x)⁴ * e^(1-x)
Ответ дал:
0
Спасибо, я еще в 11 сократила, вытащила (1-x)³ *e^(1-x) за скобки в конце :)
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад