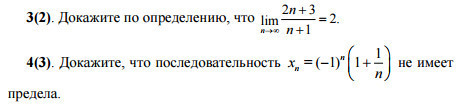Ответы
Ответ дал:
0
1) Докажем что ∀ε>0 найдется N, такое что ∀n>N |(2n+3)/(n+1) - 2| < ε
![left|frac{2n+3}{n+1}-2right| = frac{1}{n+1} textless varepsilon\
n textgreater frac{1}{varepsilon}-1\\
N = left[frac{1}{varepsilon}-1right]+1 left|frac{2n+3}{n+1}-2right| = frac{1}{n+1} textless varepsilon\
n textgreater frac{1}{varepsilon}-1\\
N = left[frac{1}{varepsilon}-1right]+1](https://tex.z-dn.net/?f=left%7Cfrac%7B2n%2B3%7D%7Bn%2B1%7D-2right%7C+%3D+frac%7B1%7D%7Bn%2B1%7D+textless++varepsilon%5C%0An+textgreater++frac%7B1%7D%7Bvarepsilon%7D-1%5C%5C%0AN+%3D+left%5Bfrac%7B1%7D%7Bvarepsilon%7D-1right%5D%2B1)
2) По модулю все члены этой последовательности больше 1, однако при каждом следующем n знак члена последовательности меняется, поэтому при любом сколь угодно большом n будут находиться члены последовательности, модуль разности которых превышает 2, что исключает попадание всех членов последовательности в малую эпсилон-окрестность какого либо числа
2) По модулю все члены этой последовательности больше 1, однако при каждом следующем n знак члена последовательности меняется, поэтому при любом сколь угодно большом n будут находиться члены последовательности, модуль разности которых превышает 2, что исключает попадание всех членов последовательности в малую эпсилон-окрестность какого либо числа
Ответ дал:
0
Ого
Ответ дал:
0
Я не глупый,но и то не разобрался в этих пределах
Ответ дал:
0
Аплодисменты
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад