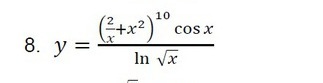Ответы
Ответ дал:
0
(2/x+x²)¹⁰ cosx
y=--------------------- обозначим функции в числителе и знамeнателе u;v
ln √x
(u/v)'=1/v²[u'v-v'u]
для нахождения u' используем обозначение rt u=rt
(rt)'=r't+t'r=[(2/x+x²)¹⁰]'cosx-(2/x+x²)¹⁰ sinx=10(2/x+x²)⁹* (-2/x²+2x)cosx-
- (2/x+x²)¹⁰ sinx =A
v=ln√x
v'=1/√x *1/2√x=1/2x
y'=(u/v)'=(1/ln²√x)[A*ln√x-(2/x+x²)¹⁰*cosx (1/2x)]
y=--------------------- обозначим функции в числителе и знамeнателе u;v
ln √x
(u/v)'=1/v²[u'v-v'u]
для нахождения u' используем обозначение rt u=rt
(rt)'=r't+t'r=[(2/x+x²)¹⁰]'cosx-(2/x+x²)¹⁰ sinx=10(2/x+x²)⁹* (-2/x²+2x)cosx-
- (2/x+x²)¹⁰ sinx =A
v=ln√x
v'=1/√x *1/2√x=1/2x
y'=(u/v)'=(1/ln²√x)[A*ln√x-(2/x+x²)¹⁰*cosx (1/2x)]
Ответ дал:
0
Спасибо)
Похожие вопросы
2 года назад
2 года назад
9 лет назад
9 лет назад