Предмет: Математика
Автор: sokolova20001
Вопрос задан 8 лет назад

Площадь параллелограмма ABCD равна 180. Точка E - середина стороны AB. Найдите площадь трапеции DAEC.

Если можно, то пример рисунка, пожалуйста.

Ответы

Ответ дал: xERISx

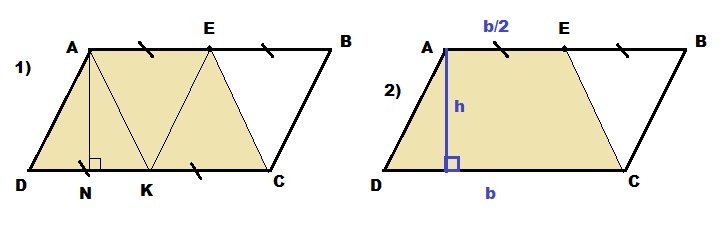
1 способ.
Так как ABCD - параллелограмм, то AD = CD.
Пусть точка К - середина стороны DC.
Так как по условию точка Е - середина стороны АВ, то
AE = BE = DK = KC ⇒
Отрезки AK, KE и EC разбивают параллелограмм на 4 равновеликих треугольника, так как в этих треугольниках равны основания и общая высота параллелограмма. ⇒
$S_{DAK}=S_{AKE}=S_{KEC}=S_{BCE}= frac{180}{4} =45$
Площадь трапеции состоит из трёх равновеликих треугольников ⇒
$S_{DAEC}=3*45=135$
-----------------------------------------------------
2 способ
Точка Е - середина стороны AB ⇒ AE = BE.
Площадь параллелограмма вычисляется по формуле
S = b*h, что по условию S = bh = 180
Площадь трапеции равна произведению полусуммы оснований на высоту.
$S_{DAEC}= frac{DC+AE}{2} *h = frac{b+b/2}{2} *h= \ \ = frac{3b/2}{2} *h= frac{3}{4}( bh)= frac{3}{4} S= frac{3}{4} *180 = 135$

Ответ: Площадь трапеции DAEC равна 135 (ед. кв)

Приложения: