Ответы
Ответ дал:
0
ДАНО
F(x) = x²/(x²+1)
НАЙТИ
Уравнение асимптоты.
РЕШЕНИЕ
Наклонная асимптота по формуле
Y = k*x + b, где коэффициент наклона

Наклонная асимптота превращается в горизонтальную.
Сдвиг по оси Y - b - по формуле
![b= lim_{x to infty} [F(x) - kx] = frac{1+ frac{1}{x^2} }{1+ frac{1}{x^2} }=1 b= lim_{x to infty} [F(x) - kx] = frac{1+ frac{1}{x^2} }{1+ frac{1}{x^2} }=1](https://tex.z-dn.net/?f=b%3D+lim_%7Bx+to+infty%7D+%5BF%28x%29+-+kx%5D+%3D++frac%7B1%2B+frac%7B1%7D%7Bx%5E2%7D+%7D%7B1%2B+frac%7B1%7D%7Bx%5E2%7D+%7D%3D1+)
Получилось уравнение горизонтальной линиии
Y = 1.
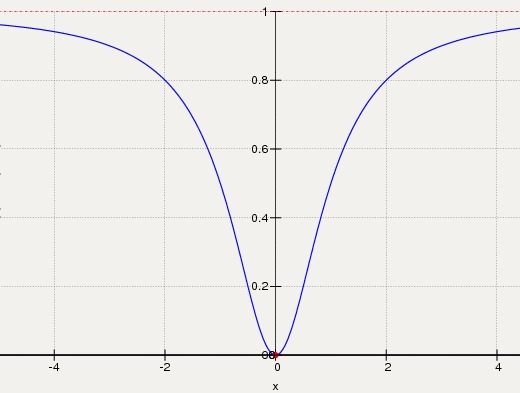
График прилагается.
F(x) = x²/(x²+1)
НАЙТИ
Уравнение асимптоты.
РЕШЕНИЕ
Наклонная асимптота по формуле
Y = k*x + b, где коэффициент наклона
Наклонная асимптота превращается в горизонтальную.
Сдвиг по оси Y - b - по формуле
Получилось уравнение горизонтальной линиии
Y = 1.
График прилагается.
Приложения:
Ответ дал:
0
это полностью выполненное задание?
Ответ дал:
0
В вопросе только асимптоты - значит полностью.
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад