Предмет: Математика
Автор: zhiltsova1
Вопрос задан 8 лет назад

< >

Найти производную функции
Y=4x3-2x2+x-5
Y=(x3-1)(x2+x+1)
Y=x2+1/x2+2

Ответы

Ответ дал: Аноним

0

смотри фото............................................

Приложения:

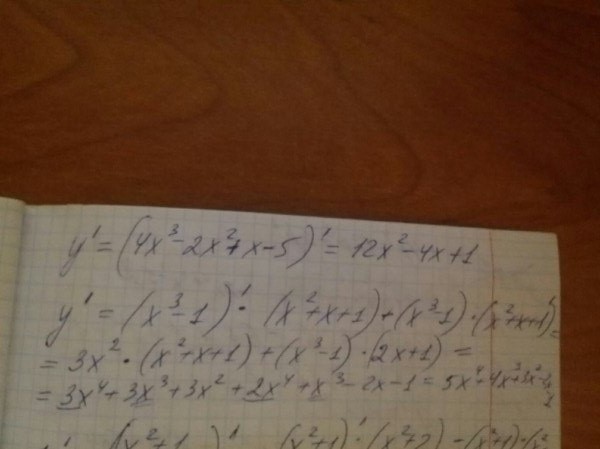
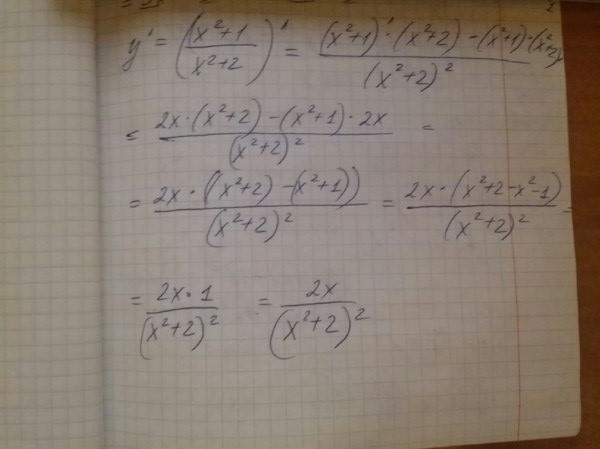
Ответ дал: TegeranUA

0

В первом у тебя ошибка в условии, а второе почему не довел до конца?

Ответ дал: Аноним

0

спасибо,описка была

Ответ дал: Аноним

0

исправила

Ответ дал: TegeranUA

0

$y'=(4x^3-2x^2+x-5)'=12x^2-4x+1 \y'=((x^3-1)(x^2+x+1))'=3x^2(x^2+x+1)+(x^3-1)(2x+1)= \=3x^4+3x^3+3x^2+2x^4+x^3-2x-1=5x^4+4x^3+3x^2-2x-1 \y'=(frac{x^2+1}{x^2+2})'=frac{2x(x^2+2)-2x(x^2+1)}{(x^2+2)^2} =frac{2x^3+4x-2x^3-2x}{(x^2+2)^2}=frac{2x}{(x^2+2)^2}$

Приложения:

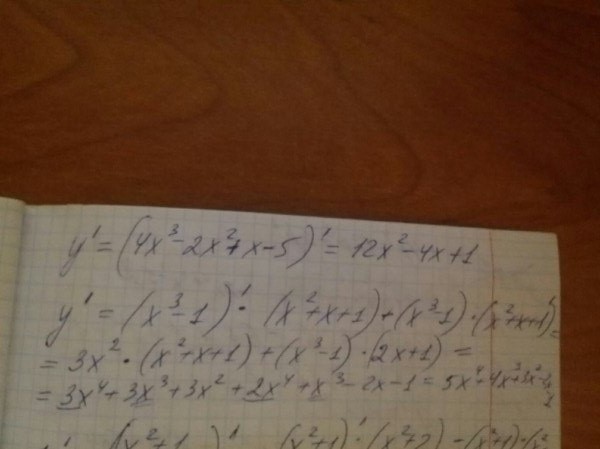
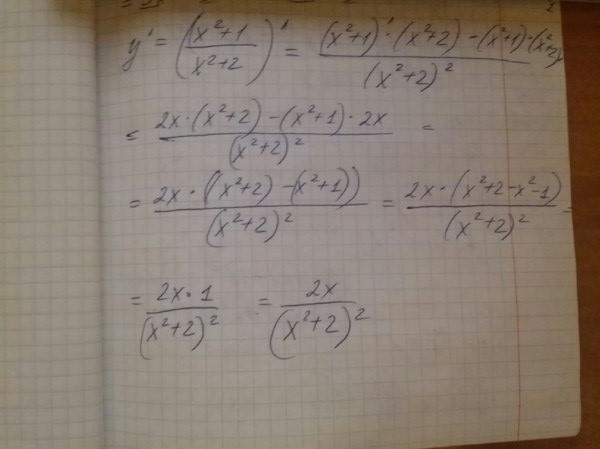
Похожие вопросы

Русский язык

2 года назад

Спишите текст определитель границы

Другие предметы

2 года назад

нарисовать сюжет из рассказа Муму

Алгебра

6 лет назад

Срочно!!! 70 баллов 1. Найди сумму минимума функции у = 2х^3 - 24х + 16 2. Найди наименьшее значение функции у = х^3 - 75х + 20 на отрезке [-1; 18] 3. Найди наибольшее значение функции у = х^2 +

История

6 лет назад

як назвали жінку-віщунку в греції

Математика

9 лет назад

запиши пропуски ...см2=6100мм2 ...дм2=650000мм2 4300см2=...дм2 760000см2=...м2 ...м2=4500дм2 ...м2=860000см2 3600дм2=...м2 850000мм2=...дм2 ...дм2=3700см2 ...см3=75000мм3 5500мм2=...см2

Физика

9 лет назад

чему равна масса ртути которой при кипении было сообщено количество теплоты 600кдж удельная теплота парообразования ртути 0.3*10в6 степини .

Алгебра

9 лет назад

Укажите какие-нибудь три корня уравнения tgx+1=0

Информатика

9 лет назад

а) машина для работы с информацией которая может применяться для многих целей: обрабатывать хранить и передавать самую разнообразную информацию использоваться в самых разных видах человеческой