Определите площадь равнобедренной трапеции, у которой длины оснований равны 10 и 26, а диагонали перпендикулярны боковым сторонам.
Ответы
Ответ дал:
0
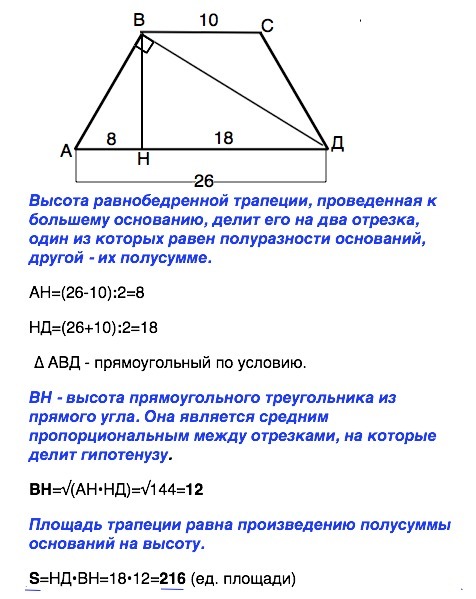
Высота равнобедренной трапеции, проведенная к большему основанию, делит его на два отрезка, один из которых равен полуразности оснований, другой - их полусумме.
АН=(26-10):2=8
НД=(26+10):2=18
∆ АВД - прямоугольный по условию.
ВН - высота прямоугольного треугольника из прямого угла. Она является средним пропорциональным между отрезками, на которые делит гипотенузу.
ВН=√(AH•HД)=√144=12
Площадь трапеции равна произведению полусуммы оснований на высоту.
S=НД•BH=18•12=216 (ед. площади)
Приложения:
Похожие вопросы
2 года назад
2 года назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад