В клетчатом квадрате 103××103 отмечены центры всех единичных квадратиков (всего 10609 точек). Какое наименьшее число прямых, не параллельных сторонам исходного квадрата, нужно провести, чтобы вычеркнуть все отмеченные точки?
Ответы
Ответ дал:
0
РЕШЕНИЕ
Используем метод дедукции.
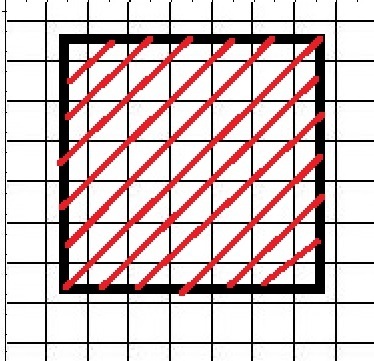
Построим квадрат - 6*6
n = 6
Косых прямых будет = 6 + 5 = 11
Или N = n+(n-1) = 2*n - 1
Для значения n = 103 получаем
N103 = 103 + 102 = 205 - ОТВЕТ
Используем метод дедукции.
Построим квадрат - 6*6
n = 6
Косых прямых будет = 6 + 5 = 11
Или N = n+(n-1) = 2*n - 1
Для значения n = 103 получаем
N103 = 103 + 102 = 205 - ОТВЕТ
Приложения:
Ответ дал:
0
а можете объяснить, почему косх линий будет 6+5? именно почему 5, а не более
Похожие вопросы
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад