Я знаю, что существует формула, позволяющая вычислить сумму всех членов бесконечно убывающей геометрической прогрессии. Но как такое возможно, если прогрессия бесконечно убывает?
Ответы
Ответ дал:
0
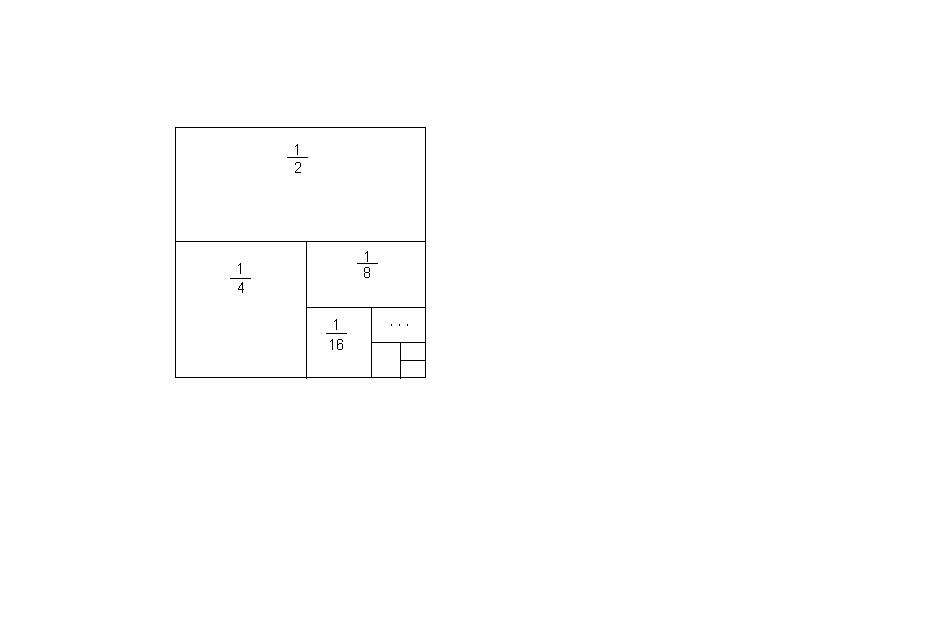
Пусть у нас есть квадрат, площадь которого равна 1.
Разделим его на две равные части. Площадь каждой 1/2.
Половину разделим еще пополам. Площадь каждой 1/4.
Четверть разделим еще пополам. Площадь каждой 1/8. И т.д. до бесконечности (см. рисунок)
Площади частей составляют геометрическую прогрессию со знаменателем 1/2, т.е. убывающую. Но сумма площадей всех этих частей равна 1!
Разделим его на две равные части. Площадь каждой 1/2.
Половину разделим еще пополам. Площадь каждой 1/4.
Четверть разделим еще пополам. Площадь каждой 1/8. И т.д. до бесконечности (см. рисунок)
Площади частей составляют геометрическую прогрессию со знаменателем 1/2, т.е. убывающую. Но сумма площадей всех этих частей равна 1!
Приложения:
Похожие вопросы
2 года назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад
9 лет назад