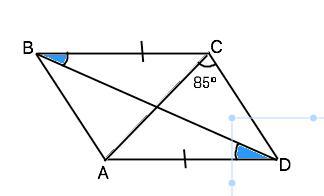
Карточка №12: На рисунке BC||AD,BC=AD. Докажите,что AB=CD. Найдите угол BAC,если угол DCA=85 градусов.

  Рисунок к вопросу не приложен. но данных для решения достаточно. Сделаем  рисунок согласно условию.

 Проведём диагональ ВD и рассмотрим ∆ ВСD и ∆ АВD.

По условию  равные ВС║АD, тогда ВD - секущая. ⇒ накрестлежащие ∠СВD=∠ВDА ⇒ ∆ ВСD=∆ АВD по первому признаку равенства треугольников ( так как  по условию ВС=АD, ВD - общая). В равных треугольниках соответственные элементы равны. Следовательно, АВ=СD. Доказано.

     Из доказанного стороны АВ и СD четырехугольника АВСD  равны. Если  в четырехугольнике противоположные стороны попарно равны, этот четырехугольник - параллелограмм. ⇒ АВ║СD, и диагональ АС при них - секущая. На этом основании накрестлежащие ∠ВАС =∠DСА ⇒. Угол BAC=85°