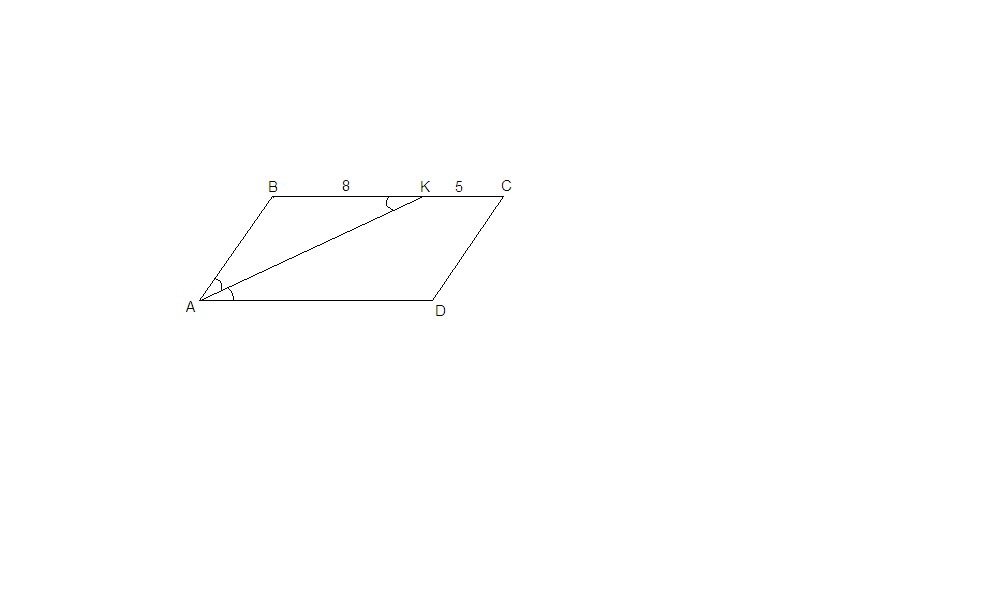
В параллелограмме ABCD биссектриса острого угла A делит противоположную сторону BC на отрезки BK=8 и KC=5. Найдите пермиетр параллелограмма ABCD

∠ВАК = ∠DAK так как АК биссектриса,
∠DAK = ∠BKA как накрест лежащие при пересечении ВС║AD секущей АК, ⇒
∠ВАК = ∠BKA, и треугольник ВАК равнобедренный:
АВ = ВК = 8.
ВС = 8 + 5 = 13

Pabcd = (AB + AD) · 2 = (8 + 13) · 2 = 42