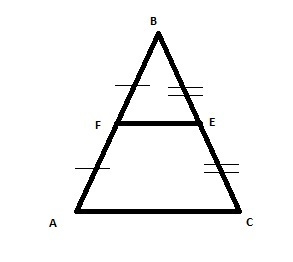
В треугольника ABC отмечены середины Е и F сторон СВ и ВА соответственно. Площадь треугольника ВЕF равна 13. Найдите площадь четырехугольника АСЕF.
(решение подробно)
Ответы
Ответ дал:
0
Так как точки Е и F являются серединами сторон ВС и ВА то EF является средней линией треугольника АВС
Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника.
Значит Sabc=Sdef*4=13*4=52
Sacef=Sabc-Sdef=52-13=39 (площадь искомого четырехугольника)
Приложения:
Похожие вопросы
2 года назад
2 года назад
6 лет назад
6 лет назад
9 лет назад
9 лет назад
9 лет назад