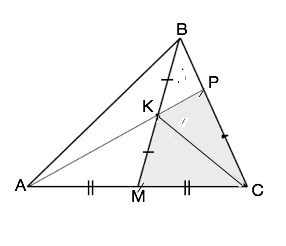
Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая,пересекающая сторону ВС в точке Р. Найдите отношение площади треугольника АВС к площади четырехугольника КРСМ

Ответы

Ответ дал: Hrisula

Медиана треугольника делит его на два равновеликих.

ВМ- медиана ∆ АВС.

Ѕ(АВМ)=Ѕ(СВМ)

АК- медиана ∆ АВМ.

Ѕ(АВК)=Ѕ(АМК)=Ѕ(АВК):2

Рассмотрим ∆ МВС с пересекающей его АР.

По т.Менелая $frac{CP}{PB}cdot frac{BK}{KM}cdotfrac{AM}{AC} =1 <br />$

$frac{CP}{PB} cdotfrac{1}{1}cdotfrac{1}{2} =1$ ⇒

СР:РВ=2:1

В ∆ МВС и ∆ ВКР угол В - общий.

Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.

Пусть ВР=х, ВК=у, тогда ВС=3х, ВМ=2у

Ѕ(МСВ):Ѕ(ВКР)=(2у•3х):ух=6:1

Примем Ѕ(ВКР)=а

Тогда Ѕ(ВМС)=6а, а Ѕ(КРСМ)=6а-а=5а

Т.к. Ѕ(АВМ)=Ѕ(ВСМ), то Ѕ(АВС)=2Ѕ(ВСМ=12а ⇒

Ѕ(АВС):Ѕ(КРСМ)=12а:5а= $frac{12}{5}$

———————

Из найденного можно найти отношение площадей любых частей ∆ АВС. Например, отношение S(ABK) ( или равновеликого ему ∆ АКМ) к площади четырехугольника KPCM равно 3а:5а=0,6

или

Ѕ(КРСМ):Ѕ(АВК)=5:3

Приложения: