Найдите все значения параметра а ,при каждом из которых неравенство
имеет единственное решение на отрезке [1;3]
Приложения:
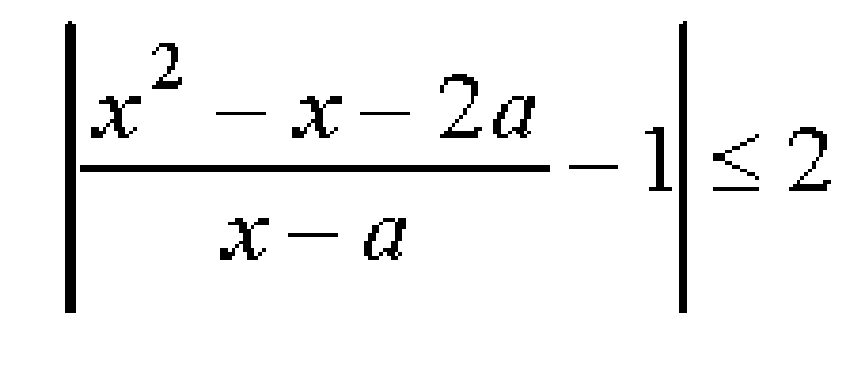
Ответы
Ответ дал:
0
Поскольку неравенство должно иметь единственное решение на отрезке, отрезки значений из нашей системы могут пересекаться с данным отрезком только в граничных точках, либо длина отрезка нашей системы долна быть равна 0 ... иными словами...
Вторая (вложенная систмеа не имеет решения, а для верхнего уравнения имеем
при а=0 значение x не попадает в установленный интервал, с другой стороны по условию a<>x (иначе знаменатель равен нулю), но при a=3 из условия
получим, что x=3 а значит x=a.
Ответ таких а не существует
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад