От квадрата со стороной 1 отрезали равнобедренный треугольник. Когда его приложили к оставшейся части квадрата, получился пятиугольник. Чему равна меньшая сторона этого пятиугольника?
(А) √2-1
(Б) 1/2
(В) √5-2
(Г) 1/3
(Д) √2+1/5
Ответы
Ответ дал:
0
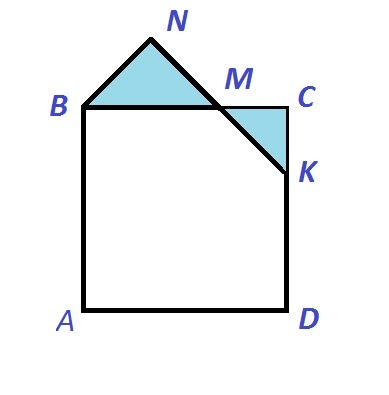
Пусть из квадрата АВСD отрезали треугольник МСК. При совмещении треугольника и квадрата получили пятиугольник АВNKD, причем его наименьшая сторона NB, которую и нужно найти.
Обозначим стороны отрезаемого треугольника CK=CM=x. После присоединения эти же стороны стали называться BN=MN=х. Искомую сторону BN обозначена за х.
Так как СМ=х, то ВМ=1-х. Но сторона BM совмещалась со стороной MK, поэтому MK=1-х.
Применяем для треугольника МСК теорему Пифагора:
![x^2+x_2=(1-x)^2
\
2x^2=1-2x+x^2
\
x^2+2x-1=0
\
D_1=1^2-1cdot(-1)=2
\
x=-1pm sqrt{2}](https://tex.z-dn.net/?f=x%5E2%2Bx_2%3D%281-x%29%5E2%0A%5C%0A2x%5E2%3D1-2x%2Bx%5E2%0A%5C%0Ax%5E2%2B2x-1%3D0%0A%5C%0AD_1%3D1%5E2-1cdot%28-1%29%3D2%0A%5C%0Ax%3D-1pm+sqrt%7B2%7D+ "x^2+x_2=(1-x)^2
\
2x^2=1-2x+x^2
\
x^2+2x-1=0
\
D_1=1^2-1cdot(-1)=2
\
x=-1pm sqrt{2}")
Отрицательной сторона быть не может, поэтому оставляем только положительный корень
.
Ответ:
Обозначим стороны отрезаемого треугольника CK=CM=x. После присоединения эти же стороны стали называться BN=MN=х. Искомую сторону BN обозначена за х.
Так как СМ=х, то ВМ=1-х. Но сторона BM совмещалась со стороной MK, поэтому MK=1-х.
Применяем для треугольника МСК теорему Пифагора:
Отрицательной сторона быть не может, поэтому оставляем только положительный корень
Ответ:
Приложения:
Ответ дал:
0
Можно ли это как-нибудь решить, если я записал как MK^2=2MC^2 и MK + BM = 1??
Ответ дал:
0
господи, что я пишу BM + CM = 1
Ответ дал:
0
Да можно, решением Пифагора
Ответ дал:
0
спасибо
Похожие вопросы
2 года назад
6 лет назад
6 лет назад
9 лет назад