Предмет: Математика
Автор: estNik
Вопрос задан 10 лет назад

< >

найдите все значения а при каждом из которых уравнение имеет единственный корень ax+ корень их -8-6x-x^2 = 2a +1

Уже сам решил :D

Приложения:

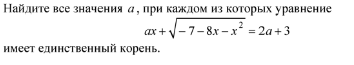
Ответы

Ответ дал: Trover

0

$ax+sqrt{-7-8x-x^2}=2a+3\ sqrt{-7-8x-x^2}=2a+3-ax\ begin{cases} -7-8x-x^2geq0\ sqrt{-7-8x-x^2}=2a+3-ax end{cases}Rightarrow\Rightarrow begin{cases} x^2+8x+7leq0\ -7-8x-x^2=(2a+3-ax)^2 end{cases}Rightarrow\ Rightarrow begin{cases} (x+1)(x+7)leq0\ -7-8x-x^2=a^2x^2-(4a^2+6a)x+(4a^2+12a+9) end{cases}Rightarrow\ Rightarrow begin{cases} xin[-7;;0]\ (a^2+1)x^2-(4a^2+6a-8)x+(4a^2+12a+16)=0 end{cases}$

$(a^2+1)x^2-(4a^2+6a-8)x+(4a^2+12a+16)=0\ D=(4a^2+6a-8)^2-4cdot(a^2+1)cdot(4a^2+12a+16)=\= 16a^4+48a^3-28a^2-96a+64-\-16a^4-48a^3-80a^2-48a-64= -108a^2-144a=0\ -108a^2-144a=0;;div36\ 3a^2-4a=0\ a(3a-4)=0\ a=0;;a=frac43$

Ответ дал: Luiiza

0

там в конце неправильно
-3а^2-4a=0
a(-3a-4)=0
a=0 a=-4/3
*^ степень

Похожие вопросы

Другие предметы

2 года назад

Объясни,кого и почему в католичестве называют Папой Римским.

Алгебра

2 года назад

Решите Логарифм срочно нужно. Нужен только ответ

Математика

7 лет назад

найдите значения выражений: 28 1/20

Математика

7 лет назад

Решите на множестве Z уравнение X-2=-5 y-25=60 z-100=-2012 Пожалуууйста

Литература

10 лет назад

Каковы особенности композиции романа "герой нашего времени"? Подготовьте ( на выбор) характеристику одного из героев княжны Мери, Веры, Вулича, Вернера, Максима максимыча. Какую роль играет эти

История

10 лет назад

обьясните термины: 1.мушкет 2. каравелла

Биология

10 лет назад

Возбудителем малярии является

Алгебра

10 лет назад

длина гипотенузы прямоугольного треугольника равна 37 см а его площадь составляет 210 см кв. найдите длины катетов